Kretser i frekvensdomenet

Forelesning.

Kretser i frekvensdomenet

(Lærebok 15.3.1)

Oppgave.

Oppgave: Komplekse tall

La oss kort repetere komplekse tall.

a) Hva er $ |2 + i| $?

Answer.

$ \sqrt{5} $

Solution.

Det er $$ \begin{equation} \left(|2|^2 + |i|^2 \right)^{1/2} = \sqrt{5} \; . \tag{4} \end{equation} $$

b) Tegn $ 2+i $ i det komplekse planet.

Solution.

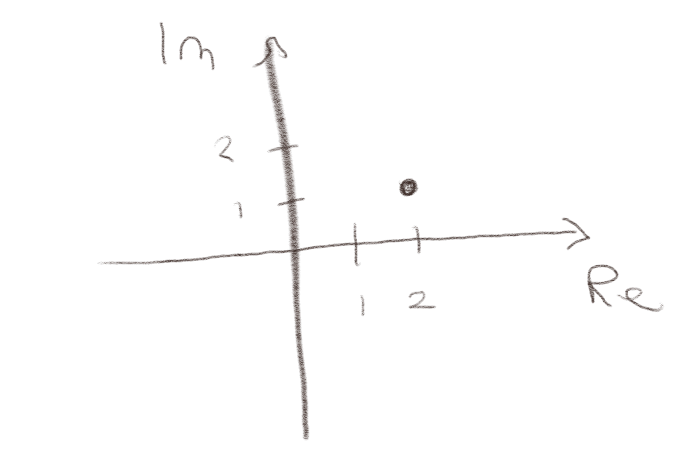
c) Hvordan kan vi skrive $ 2+i $ som $ Ae^{i \phi} $?

Solution.

Vi kan skrive den på denne formen ved å skrive $ A = |2 + i| $ og å velge $ \phi $ slik at $$ \begin{equation} \tan \phi = \frac{\text{Im}\{ 2+i \} }{\text{Re}\{ 2+i \} } = \frac{1}{2} \; , \tag{5} \end{equation} $$ som gir at $ \phi = \arctan (1/2) $.

Oppgave.

Oppgave: Hvilket signal kommer først?

Figuren viser strømmen og spenningen i en krets.

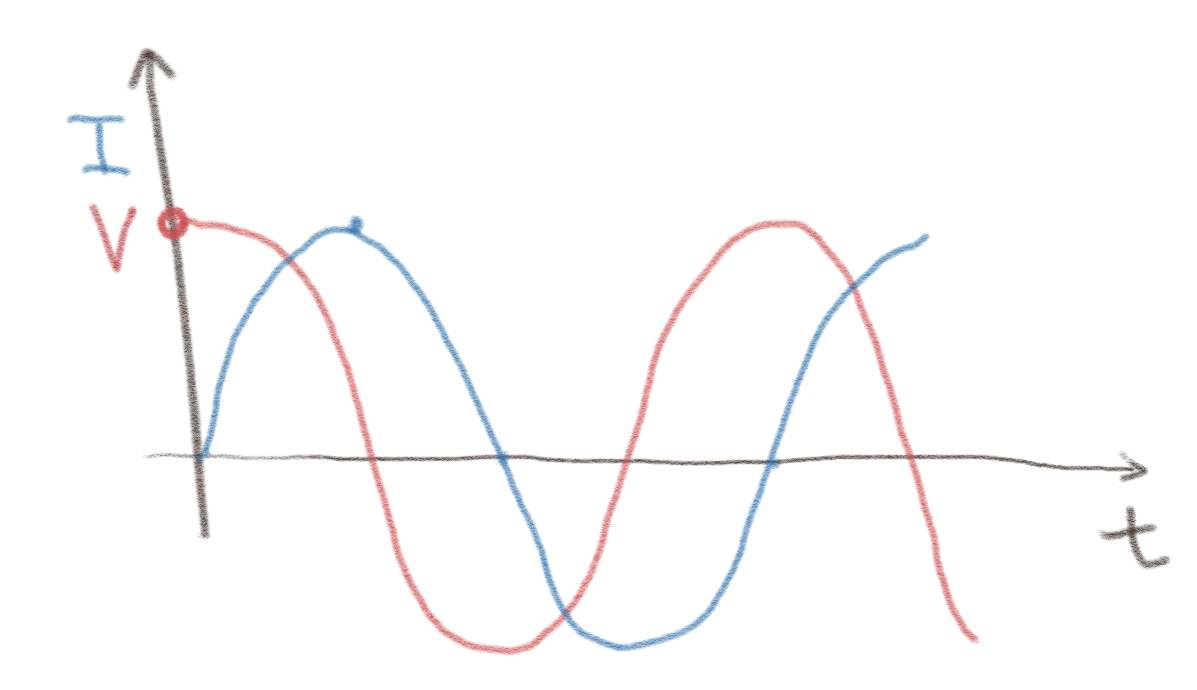
a) Ligger $ V $ før $ I $ eller $ I $ før $ V $?

Solution.

Dette havner i hovedsak om hvordan vi leser av denne figuren. Vi ser at $ V $ har et maksimum før $ I $. Vi sier derfor at $ V $ ligger før $ I $. Men det avhenger jo av hvordan man ser det. Vi kan jo også si at $ I $ ligger før $ V $.

b) Hvor stor er forskjellen i fase?

Solution.

Vi antar at signalene har en sinus-form. Vi ser at strømmen $ I $ er maksimal når $ V $ er null. Vi antar at $ V = 0 $ når fasen er $ \pi/2 $. Det betyr at faseforskjellen er $ \pi/2 $.

c) Hvis $ V = V_0 e^{i \omega t} $ hva er er da $ I $?

Solution.

Real-verdien av $ V $ er $ V_0 \cos \omega t $ som stemmer overens med figuren. Vi antar at $ I = I_0 \cos (\omega t + \delta) $. Vi ser da at $ I $ når den samme verdien som $ V $ men med en faseforskjell på $ \pi/2 $. Det betyr at når $ t=0 $ så skal argumentet for $ I $ være $ -\pi/2 $ slik at $ \delta = - \pi/2 $.

Eksempel.

Eksempel: Kompleks representasjon av en motstand

(Lærebok 15.3.2)

Eksempel.

Eksempel: Kompleks representasjon av en kondensator

(Lærebok 15.3.3)

Eksempel.

Eksempel: Kompleks representasjon av en spole og regler for impedans

(Lærebok 15.3.4)

Oppgave.

Oppgave: Fasevinkel

For en spole er $$ \begin{equation} I_0 e^{i \delta} = \frac{V_0}{i \omega L} = \frac{V_0}{\omega L} e^{i \delta} \; . \tag{6} \end{equation} $$

a) Hva er fasevinkelen $ \delta $?

Answer.

$ -\pi/2 $.

Solution.

I dette tilfellet ser vi at $$ \begin{equation} \frac{V_0}{i \omega L} = \frac{V_0}{\omega L} (-i) = \frac{V_0}{\omega L} e^{i \delta} \; . \tag{7} \end{equation} $$ Vi ser derfor at $ e^{\delta} = -i $ og dermed er $ \delta = -\pi/2 $.

Eksempel.

Eksempel: RC-krets i frekvensdomenet

(Lærebok 15.3.6)

Oppgave.

Oppgave: Total impedans

Figuren viser en krets med en periodisk spenningskilde.

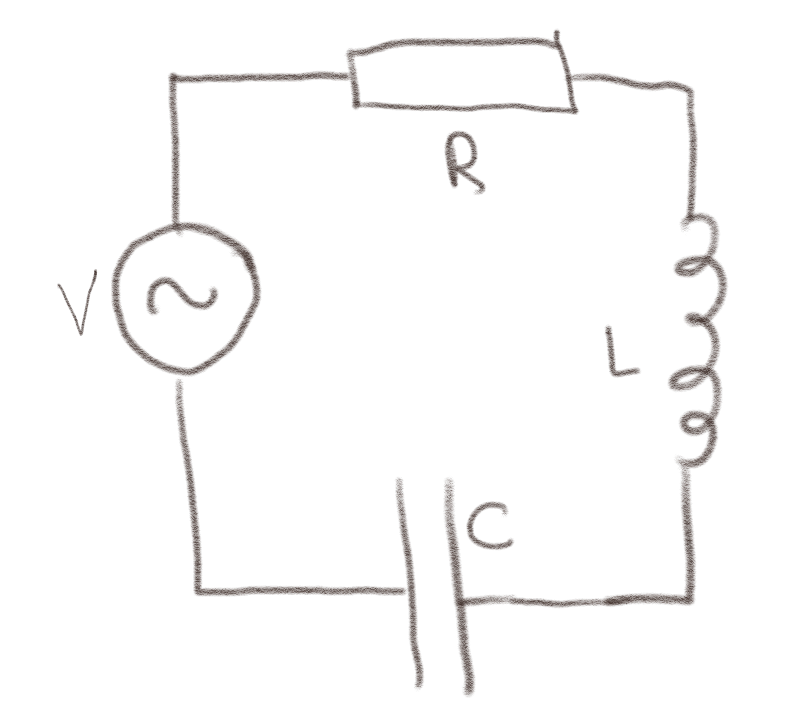
a) Hva er en den totale impedansen til kretsen?

Solution.

Impedansen til hvert enkelt element er $$ \begin{equation} Z_R = R \quad , \quad Z_C = \frac{1}{i \omega C} = \frac{-i}{ \omega C}\quad , \quad Z_L = i \omega L \; . \tag{8} \end{equation} $$ Alle impedansenen er koblet i serie. Vi finner derfor den totale impedansen som $$ \begin{equation} Z_T = Z_R + Z_C + Z_L = R + i \left( \omega L - \frac{1}{\omega C} \right) \; . \tag{9} \end{equation} $$