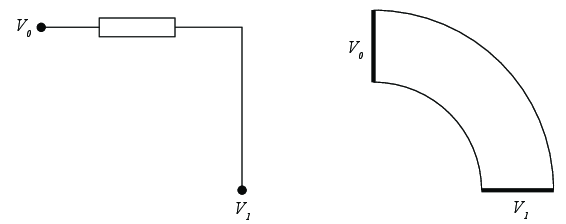
Oppgave
Oppgave: Strøm og spenning i en elektrisk leder
Figuren viser en elektrisk ikke-ideell leder formet som en rett leder (til venstre) og en fjerdedel av et sylinderskall (til høyre). (Vi antar systemet har en liten tykkelse inn i planet). Det en en spenningsforskjell mellom endeflatene som vist i figuren, \( V_1>V_0 \).
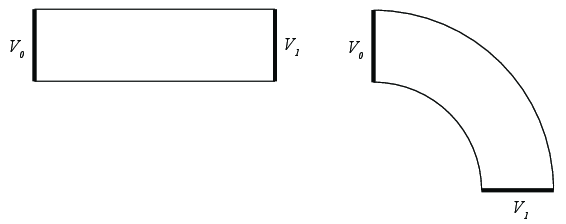
a) Skisser det elektriske feltet inne i den rette lederen (til vestre).
Det er homogent og peker fra høy mot lav spenning.
b) Skisser ladningsfordelingen når det går en strøm i den rette lederen (til venstre).
Tenk deg at dette er en motstand. Hvordan er da det elektriske feltet og hvordan er ladningsfordelingen som lager dette elektriske feltet?
Det er positiv ladning som er uniformt fordelt på den svarte overflaten ved potensialet \( V_1 \) og negativ ladning ved \( V_0 < V_1 \) som er uniform fordelt på den svarte overflaten.
Du bøyer så den rette lederen til den får formen vist til høyre.
c) Hvordan blir det elektriske feltet inne i lederen?
Det elektriske feltet vil peke langsmed lederen inne i lederen, fra høyt til lavt potensiale/spenning.
d) Hvordan blir nå ladningsfordelingen i lederen?
Det er fremdeles ladningsfordelingen som setter opp det elektriske feltet inne i lederen.
Litt mer tricky, men ladningsfordelingen vil gå fra positive ladninger nær \( V_1 \) til negative ladninger nær \( V_0 \) på et slikt vis at det elektriske feltet overalt peker langsmed lederen.
e) Må det elektriske feltet utenfor lederen være null?
Nei - og det vil det generelt heller ikke være.
f) (Litt vanskelig for de som vil ha en liten nøtt) Er det elektriske feltet homogent inne i den bøyde lederen?
Velg deg en sirkelformet bane med konstant radius fra den ene enden til den andre. Hva blir integralet av det elektriske feltet langs denne banen? Hva forteller det deg om det elektriske feltet?
Her kan man bruke flere fremgangsmåter. Vi kan anta at det elektriske feltet kun har en \( \phi \)-komponent som avhenger av \( r \) slik at \( E = E_{\phi}(r) \). Vi integrerer over en vinkel \( \phi_0 \) og får $$V_0 - V_1 = \int_0^{\phi_0} E_{\phi}r \d \phi = E_{\phi} r \phi_0 = V_0 - V_1$$ slik at $$E_{\phi} = \frac{V_0 - V_1}{r \phi_0}$$ hvor vi også ser at vi har riktig fortegn (negativt)! Et annet alternativ kan være å anta at potensialet er \( V(\phi) = V_0 + (V_1-V_0)\phi_0 \phi \) som stemmer med grensebetingelsene. Da kan man finne det elektriske feltet i sylinderkoordinater.
g) Hvordan vil du modellere dette systemet som en elektrisk krets? Tegn kretsen.
Du skal gjøre om systemet til en eller flere krets-komponenter som er koblet sammen med ideelle ledere som vi tegner som streker.