Coulombs lov
Introduksjon til Coulombs lov
(Lærebok 1.1.0-1.1.1)
Oppgave: Krefter
Question: The net force on a system due to all the electrostatic forces between charges in the system is zero. Is this statement true or false? Explain your answer.
Correct!
Wrong!
Oppgave: Krefter del 2
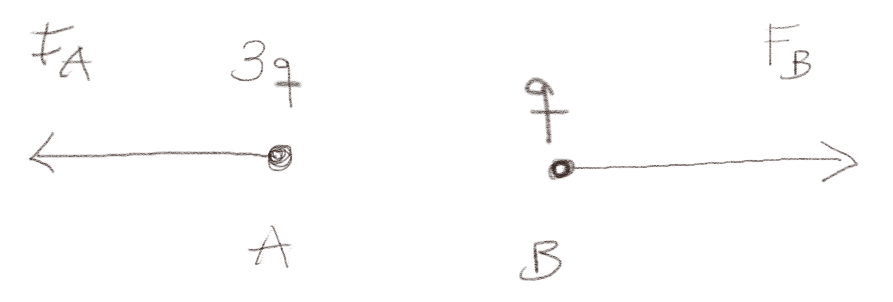
Question: What is the relation between the force \( F_A \) on charge A and \( F_B \) on charge B?
Correct!
Wrong!
Wrong!
Oppgave: Ladninger
a)
5
Vi finner netto ladning ved å summere positive og negative ladninger.
- Glasset som mangler tre elektroner har derfor en positiv ladning på \( 3e \).
- Et proton har ladning på \( e \)
- Et system med like mange positive og negative ladning har ladning 0
- Et elektron har ladning på \( -e \)
- 17 protoner og 19 elektroner gir netto ladning på \( -2e \)
Eksempel: Krefter på en ladning
(Lærebok 1.1.1)
Oppgave: Kraft mellom ladninger
En ladning \( Q \) ligger i \( (a, 0) \). Du skal finne kraften fra ladningen \( Q \) på en ladning \( q \) i \( (0,a) \):
a) Hva er \( \vec{R} \)?
\( (-a,a) \)
Vi ser at \( \vec{r} = (0,a) \) or \( \vec{r}_1 = (a,0) \) slik at \( \vec{R} = \vec{r} - \vec{r}_1 = (-a,a) \).
b) Hva er kraften fra \( Q \) på \( q \)?
\( \vec{F} = \frac{qQ}{4 \pi \epsilon_0}\frac{(-a,a)}{a^3 2^{3/2}} \)
Vi finner $$ \begin{equation} \vec{F} = \frac{qQ}{4 \pi \epsilon_0}\frac{\vec{R}}{R^3} = \frac{qQ}{4 \pi \epsilon_0}\frac{(-a,a)}{a^3 2^{3/2}} \; . \tag{1} \end{equation} $$