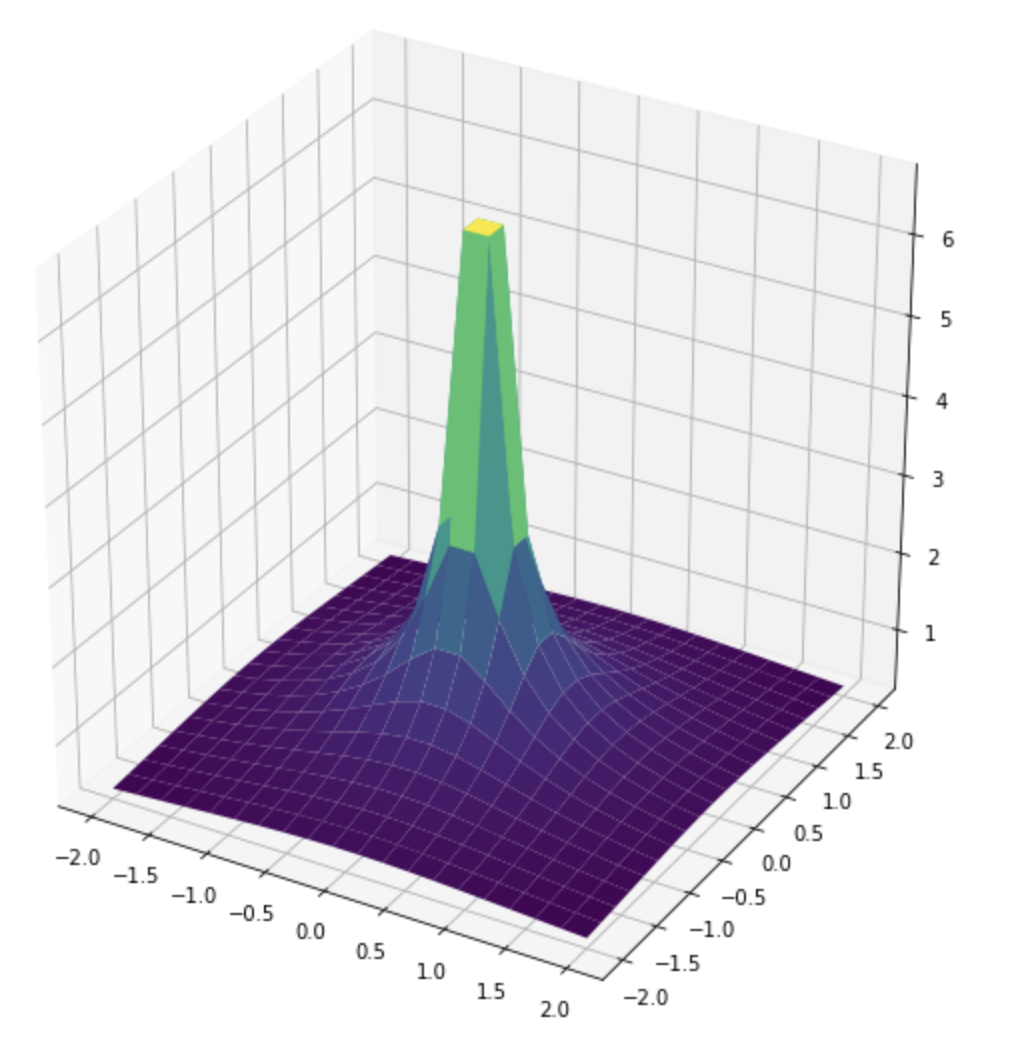
A positive charge at \( (0,0) \).

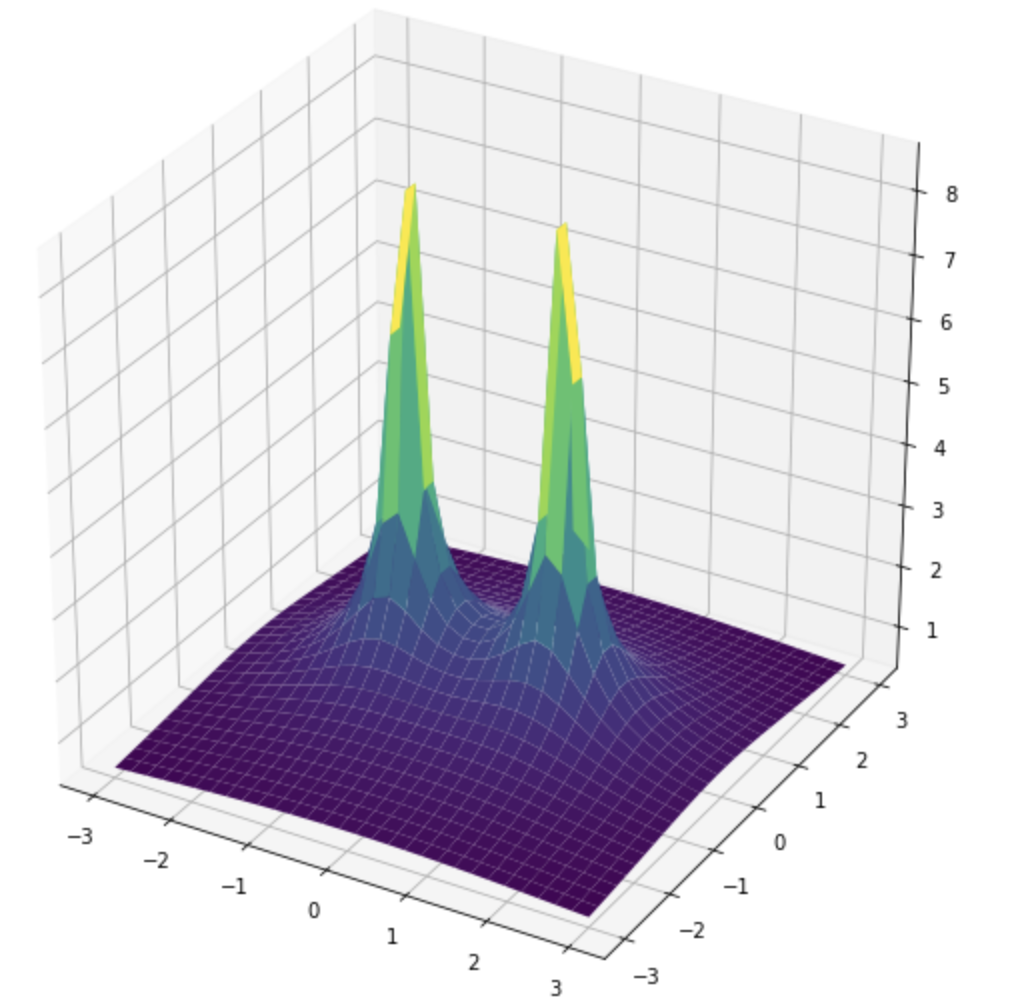
Two positive charges at \( (1,0) \) and \( (-1,0) \).

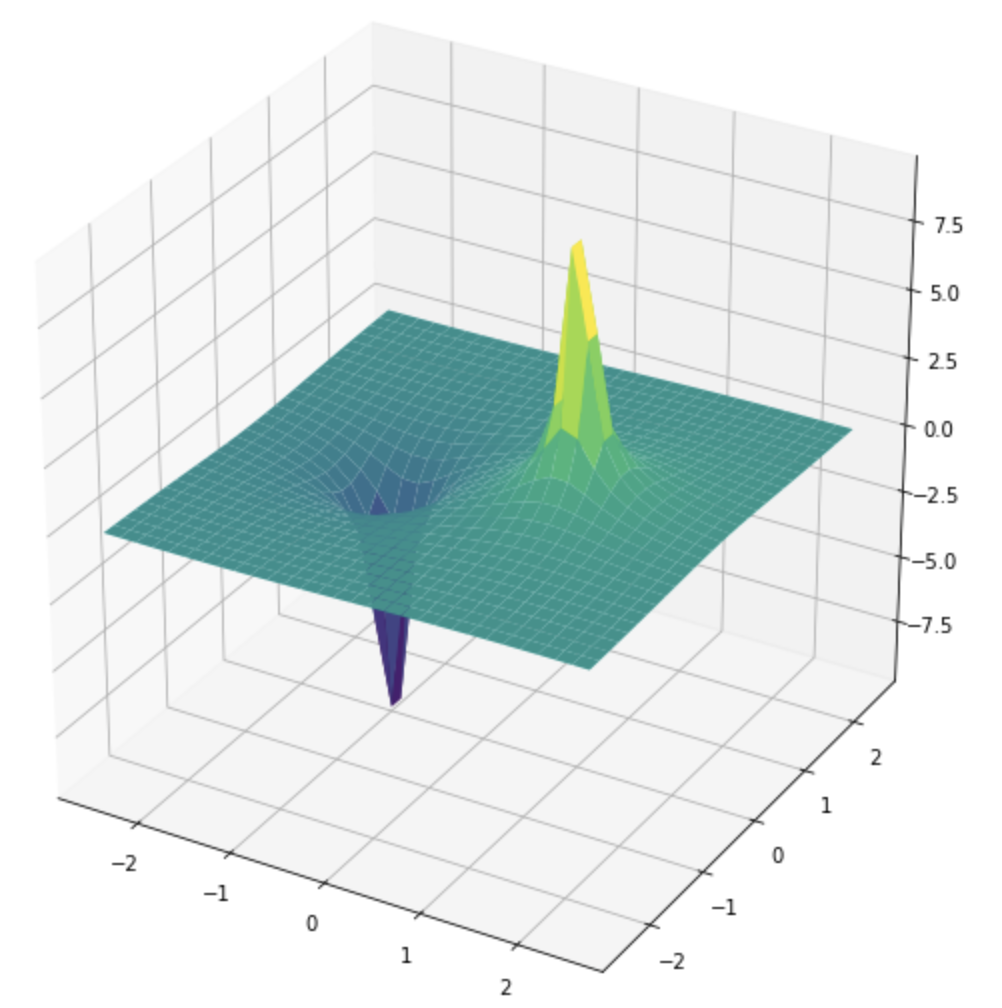
A positive charge at \( (1,0) \) and a negative charge of equal magnitude at \( (-1,0) \).

\( V(x,y) = 0 \)

There are no charges in this area. The electric scalar potential must satisfy Laplace equation \( \nabla^2 V = 0 \) with boundary conditions \( V(0,y) = 0 \) and \( V(L,y) = 0 \). The system is symmetric along the \( y \)-axis. We will therefore not have any \( y \)-dependence. Thus Laplace equation is \( \partial^2 V/\partial x^2 = 0 \). This has the solutions \( V(x) = Ax + B \). The boundary conditions gives that \( A = B = 0 \), and therefore \( V(x,y) = 0 \) for this system.

\( V_1(x) = 2 V_1 x/L \) and \( E_1(x) = -2 V_1/L \) for \( 0 < x < L/2 \); \( V_2(x) = 2 (V_1/L) (L/2-x) + V_1 \) and \( E_2(x) = 2 V_1/L \) for \( L/2 < x < L \).

The system is still described by \( V(x,y) = A_ix + B_i \) in each of the regions (1) \( 0 < x < L/2 \) and (2) \( L/2 < x < L \). For the region \( 0 < x < L/2 \), the boundary conditions \( V(0) = 0 \) gives \( A_1 \cdot 0 + B_1 = 0 \) and therefore \( B_1 = 0 \). The other boundary condition \( V(L/2) = V_1 \) gives \( A_1(L/2) = V_1 \) and \( A_1 = 2 V_1 /L \), thus \( V(x) = 2 V_1 x/L \).

For the range \( L/2 < x < L \) we have that \( V(L) = 0 = A_2 L + B_2 \) and that \( V(L/2) = A_2 (L/2) + B_2 = V_1 \). Thus \( V(x) = 2 (V_1/L) (L/2-x) + V_1 \)

The electric field is \( E_1(x) = -\partial V/\partial x = -2 V_1/L \) for \( 0 < x < L/2 \) and \( E_2(x) = 2 V_1/L \) for \( L/2 < x < L \).

A conductor with potential \( V_1 \) at \( x=L/2 \) and conductors at \( V=0 \) at \( x=0 \) and \( x=L \). (It can also be a sheet of charge at \( x=L/2 \). What would the charge be?)

\( \rho_a = 2 V_1 \epsilon/L \) on each side of \( x=L/2 \) and \( \rho_a = -2 V_1 \epsilon/L \) at \( x=0 \) and \( x=L \).

The surface charge density is given by the field, \( E_n = 2V_1/L = \rho_a/\epsilon \), and therefore \( \rho_a = 2 V_1 \epsilon/L \) at \( x=L/2 \) (on each side) and \( \rho_a = -2 V_1 \epsilon/L \) at \( x=0 \) and \( x=L \).

\( E=0 \) for \( r < a \) and \( \vec{E} = Q/(4 \pi \epsilon r^2) \hat{r} \) for \( r > a \).

We can use Gauss' law. We assume that the field will have spherical symmetry. Inside the sphere, there will be no charge inside a spherical surface, hence the flux and the field is zero. Outside the sphere, the flux is \( 4 \pi \epsilon R^2 E = Q \), and therefore \( E = Q/(4 \pi \epsilon R^2) \).

\( V(r) = Q/(4 \pi \epsilon r) \) for \( r > a \) and \( V(r) = Q/(4 \pi \epsilon a) \) for \( r \le a \).

The scalar potential is found from \( V(r) = \int_r^{\infty} E(r) \, dr = Q/(4 \pi \epsilon r) \) for \( r > a \). When \( r < a \) the field is zero, hence the potential is the same inside the sphere as on the sphere boundary, \( V=Q/(4 \pi\epsilon a) \).

We find the \( \nabla^2 \) operator for spherical coordinates from the formula collection: $$ \begin{equation} \nabla^2V = \frac{1}{r^2} \frac{\partial}{\partial r} \left( r^2 \frac{\partial V}{\partial r} \right) + \frac{1}{r^2 \sin \theta}\frac{\partial}{\partial \theta} \left( \sin \theta \frac{\partial V}{\partial \theta } \right) + \frac{1}{r^2 \sin^2 \theta} \frac{\partial^V}{\partial \phi^2} \; . \tag{5.2} \end{equation} $$ Here, \( V \) has no \( \theta \) or \( \phi \) dependence. Hence, we insert the solution into \( \nabla^2 V \). We start from the inside: $$ \begin{equation} \frac{\partial V}{\partial r} = \frac{\partial}{\partial r} \frac{Q}{4 \pi \epsilon r} = -\frac{Q}{4 \pi r^2} \tag{5.3} \end{equation} $$ We see that if we multiply with \( r^2 \) we get a constant, and hence \( \nabla^2 V = 0 \).

For \( r < a \) the solution is constant and hence trivially satisfies Laplace equation.

\( \rho_a = Q/(4 \pi a^2) \)

We know that the change in field across \( r=a \) corresponds to the surface charge here: \( D_{2n} - D_{1n} = \rho_a \). Immediately inside the field is zero, and immediately outside it is \( D = E\epsilon = Q/(4 \pi \epsilon a^2)\epsilon = Q/(4 \pi a^2) \). Hence the surface charge density is \( \rho_a = Q/(4 \pi a^2) \), which is indeed what we could recognize immediately.

\( x(t) = t \, 10 \text{m/s} - \frac{t^2}{2} 10 \text{m/s}^2 \)

The general solution is that \( x(t) = x_0 + v_0 t + \frac{1}{2}gt^2 \), which gives \( x(t) = t \, 10 \text{m/s} - \frac{t^2}{2} 10 \text{m/s}^2 \).

\( V(x) = x \, 10 \text{V/m}^2 - \frac{x^2}{2} 10 \text{V/m}^3 \)

The solution to Poisson's equation \( d^2/dx^2 = -\rho_0/\epsilon_0 \) must have the form $$ \begin{equation*} V(x) = Ax^2 + Bx + C \end{equation*} $$ where the coefficient \( A \) is determined by Poisson's equation, because \( \nabla^V = 2A = -10 \text{V/m}^3 \), and \( A = -\frac{1}{2}10 \text{V/m}^3 \). $$ \begin{equation*} V(x) = C + Bx -\frac{1}{2}10 x^2 \; . \end{equation*} $$ We determine \( B \) and \( C \) from the boundary conditions: \( V(0) = C = 0 \) and \( V(2) = 2B - 5\, 4 = 0 \), which gives \( B = 10\text{V/m}^2 \). The solution is therefore $$ \begin{equation*} V(x) = x \, 10 \text{V/m}^2 - \frac{x^2}{2} 10 \text{V/m}^3 \; . \end{equation*} $$

The boundary condition \( V(0)= 0 \) still gives that \( C=0 \). However, we now find that \( V(2) = 2B -20 = 2 \), which gives that \( B = 11 \text{V/m}^2 \). The solution is therefore $$ \begin{equation*} V(x) = x \, 11 \text{V/m}^2 - \frac{x^2}{2} 10 \text{V/m}^3 \; . \end{equation*} $$

\( v_0 = 11\text{m/s} \)

Yes, \( C = 0 \) and \( B = (V(2)+20)/2 \text{V/m}^2 \).

The initial value problem is simple to solve numerically, since we simply step forward in time from the intial values. However, the boundary value problem is more tricky. We cannot start from \( x=0 \), because we do not know \( V'(0) \). Instead, we know where we should get after a given number of steps: \( V(0) = 0 \) and \( V(x_1) = V_1 \).

Hmmm. We need to approach this problem in a different way. One way is to discretize the equation $$ \begin{align*} \frac{d^2 V}{d x^2} &\simeq \frac{1}{\Delta x}\left( \frac{V(x+ \Delta x)-V(x)}{\Delta x} - \frac{V(x)-V(x-\Delta x)}{\Delta x} \right) \\ &\simeq \frac{V(x + \Delta x) + V(x-\Delta x) - 2 V(x)}{\Delta x^2} = - \rho(x)/\epsilon_0\; . \end{align*} $$ Let us introduce \( x_i = i \Delta x \) and \( V_i = V(x_i) \) so that \( V_0 \) is the boundary condition at \( x=0 \) and \( V_{N+1} = V_1 \) is the boundary condition at \( x_1 \). We can then list the equations as $$ \begin{align*} V_2+V_0-2V_1 &= -\Delta x^2 \, \rho(x_1)/\epsilon_0 \\ V_3+V_1-2V_2 &= -\Delta x^2 \, \rho(x_2)/\epsilon_0 \\ V_4+V_2-2V_3 &= -\Delta x^2 \, \rho(x_3)/\epsilon_0 \\ \ldots &= \ldots \\ V_{N}+V_{N-2}-2V_{N-1} &= -\Delta x^2 \, \rho(x_{N-1})/\epsilon_0 \\ V_{N+1}+V_{N-1}-2V_N &= -\Delta x^2 \, \rho(x_N)/\epsilon_0 \\ \end{align*} $$

This means that to solve this problem numerically, we need to solve this system of equations for \( V_i \). This is rather different than solving the problem with initial conditions.

\( 3\cdot 10^4 \) V

For at det skal oppstå gjennomslag må spenningen være større enn \( V_{tl} = E_{tl} d = 3\cdot 10^4 \) V

\( 6\cdot 10^4 \) V

Dette dielektriske mediet vil gi større spenningstoleranse fordi det tåler en høyere spenning: \( V_{tp} = E_{tp}d = 6\cdot 10^4 \) V. Det er også verdt å merke seg at det å legge inn et dielektrikum vil føre til at ladningen på kondensatorplaten vil øke med en faktor \( \epsilon_r \).

Dette endrer situasjonen dramatisk, siden vi nå får en grenseflate mellom porselen og luft. Vi vet at \( D \)-feltet ikke bryr seg om permittiviteten til materialet, så vi kommer til å ha et konstant \( D \)-felt mellom platene. Dermed får vi at \( E_p = \frac{E_l}{\epsilon-r} \). Vi setter så opp uttrykket for spenningsfallet mellom metallplatene: $$ \begin{equation} V = E_l(d-d_p) + E_p d_p = E_l \left[ d-d_p \left(1-\frac{1}{\epsilon_r}\right)\right] \tag{5.4} \end{equation} $$

Siden \( E_p = \frac{E_l}{\epsilon-r} \) kommer vi til å ha det sterkeste \( E \)-feltet i lufta, og siden lufta attpåtil tåler mindre felt enn porselenet er det gjennomslag i lufta vi trenger å bekymre oss for. Derfor er den høyeste spenningen som kan tåles $$ \begin{align} V_{t} &= E_{tl} \left[ d-d_p \left(1-\frac{1}{\epsilon_r}\right)\right] \tag{5.5}\\ &= 3\times 10^6 \text{ V/m} \cdot (0.01\text{ m} -0.009\text{ m} \cdot (1-1/7)) \tag{5.6}\\ &= 6857 \text{ V} \tag{5.7} \end{align} $$

Dette er mye mindre enn vi tålte med bare luft imellom, og det skyldes at det dielektriske materialet tar mindre av spenningsfallet mellom platene pga høyere permittivitet. Dermet tvinges luften til å ta det meste av spenningsfallet, og det over en mye mindre distanse enn tidligere, slik at feltet blir større.

Poissons ligning gir en 2. ordens differensiallikning i en variabel. Løs denne med grensebetingelsene \( V(0) = V_0 \) og \( V(d) = 0 \).

Poissons likning er \( \nabla^2 V = -\frac{\rho}{\epsilon} \). Siden platene er store antar vi at \( V \) kun kommer til å være en funksjon av \( x \), slik at poissons likning reduseres til $$ \begin{equation} \frac{\partial^2 V}{\partial x^2} = -\frac{\rho}{\epsilon} \tag{5.8} \end{equation} $$ der \( \rho \) og \( \epsilon \) er konstanter i denne oppgaven.

Vi integrerer likningen to ganger, og får at $$ \begin{equation} V(x) = -\frac{\rho x^2}{2\epsilon} + c_1 x + c2. \tag{5.9} \end{equation} $$

Grensebetingelsene gir oss $$ \begin{align} V(0) &= c_2 = V_0 \tag{5.10}\\  V(d) &= -\frac{\rho x^2}{2\epsilon} + c_1 d + V_0 \tag{5.11} \end{align} $$ altså $$ \begin{align} c_1 &= \frac{\rho d}{2\epsilon} - \frac{V_0}{d} \tag{5.12}\\ c_2 &= V_0 \tag{5.13} \end{align} $$ Vi setter dette inn i den generelle løsningen og får $$ \begin{equation} V(x) = -\frac{\rho x^2}{2\epsilon} + \left(\frac{\rho d}{2\epsilon} - \frac{V_0}{d}\right)x + V_0 \text{ for } x \in [0,d] \tag{5.14} \end{equation} $$

I elektrostatikken er generelt \( E=-\nabla V \). Siden vi har et endimensjonal system reduseres dette til $$ \begin{equation} \mathbf{E} = -\frac{\d V}{\d x}\x = \left[ \frac{\rho x}{\epsilon} - \left( \frac{\rho d}{2\epsilon} - \frac{V_0}{d} \right)\right]\x \tag{5.15} \end{equation} $$

Om vi setter inn for verdiene oppgitt i oppgaven, i tillegg til \( \epsilon = \epsilon_0 \approx 8.854 \cdot 10^{-12} \) F/m siden luft har omtrent samme permittivitet som vakuum, får vi $$ \begin{equation} \mathbf{E} \approx (-1.13 x+6.65)\x \text{ V/mm} \tag{5.16} \end{equation} $$

\( V_{\text{min}} = -9.57 \) V

Potensialet \( V \) har ekstremalverdier der \( \frac{\d V}{\d x} = 0 \), dvs. \( E(x) = 0 \), som gir $$ \begin{equation} \frac{\rho x}{\epsilon} - \left( \frac{\rho d}{2\epsilon} -\frac{V_0}{d} \right) = 0. \tag{5.17} \end{equation} $$ Når vi løser denne likningen for \( x \) får vi $$ \begin{equation} x_{ekstremal} = \frac{2}{2}-\frac{V_0\epsilon}{\rho d} \approx 5.89 \text{ mm} \tag{5.18} \end{equation} $$

Vi ser at \( E \)-feltet er positivt til venstre for dette punktet, og negativt til høyre for dette punktet. Siden \( E = -\frac{\d V}{\d x} \) kan vi dermed konkludere at \( x_{ekstremal} \) er et bunnpunkt for potensialet. Dersom det var et topppunkt måtte vi ha lett etter ekstremalpunkter på randen av området.

Vi evaluerer \( V(x) \) i \( x_{min} = 5.89 \) mm, og finner at $$ \begin{equation} V_{min} = V(x_{min}) = -9.57 \text{ V} \tag{5.19} \end{equation} $$

Figuren under viser potensialet og feltet.

Koden som genererer plottet:

import numpy as np 
import matplotlib.pyplot as plt

def V(x, d=0.01, V0=10, Vd=0, epsilon=8.854e-12, rho=-1e-5):
    return -rho*x**2/(2*epsilon) + (rho*d/(2*epsilon) - V0/d)*x + V0

def E(x, d=0.01, V0=10, Vd=0, epsilon=8.854e-12, rho=-1e-5):
    return rho*x/epsilon - (rho*d/(2*epsilon) - V0/d)

x = np.linspace(0, 0.01, 100)


plt.figure(figsize=(6, 6))
plt.subplot(211)
plt.axhline(0, color="k")
plt.plot(x*100, V(x))
plt.plot([0, 0.589], [-9.57, -9.57], "k--", linewidth=1)
plt.plot([0.589,0.589], [-9.57,0], "k--", linewidth=1)
plt.text(0.589, -10, "$V_{min} = -9.57$ V", verticalalignment="top", horizontalalignment="center")
plt.text(0.589, 1, "$x_{min}=5.89$ mm",horizontalalignment="center")
plt.ylim([-13, 11])
plt.xlabel("x (cm)")
plt.ylabel("V (V)")
plt.subplot(212)
plt.axhline(0, color="k")
plt.plot(x*100, E(x)/1000)
plt.plot([0,1], [0,0], "k--")
plt.plot([0.589,0.589], [-0.2,0.2], "k-")
plt.text(0.589, 1, "$x_{min}$",horizontalalignment="center")

plt.xlabel("x (cm)")
plt.ylabel("E (V/mm)")
plt.tight_layout()

Vi deler opp staven i små biter og bruker Coulombs lov på hver av de små bitene. $$ \begin{equation} \mathbf{E} = \lim_{\Delta x \to 0} \sum_i \frac{\rho_l \Delta x_i}{4\pi \epsilon_0 r_i^2} \frac{\rvec_i}{r_i} \tag{5.20} \end{equation} $$ Der summen er slik at den får med seg hele staven fra \( -L \) til \( L \).

Dette er nøyaktig definisjonen av følgende integral: $$ \begin{equation} \int_{-L}^L \frac{\rho_l \d x}{4\pi\epsilon_0 r^2}\frac{\rvec}{r} \tag{5.21} \end{equation} $$

der \( \rvec = -x\x + z\z \), altså vektoren som peker fra ladningen \( \rho_l \d x \) og mot punktet der vi ønsker å beregne feltet, og \( r = |\mathbf{r}| = \sqrt{x^2+z^2} \). Dermed blir integralet $$ \begin{equation} \mathbf{E} = \int_{x=-L}^L \frac{\rho_l \d x}{4\pi\epsilon_0 (x^2+z^2)^\frac{3}{2}}(-x\x + z\z) \tag{5.22} \end{equation} $$ Siden (-x) er antisymmetrisk på integrasjonsområdet \( [-L, L] \), og resten av uttrykket er symmetrisk på det samme området, kommer \( x \)-komponenten av feltet til å kansellere. Derfor ser vi bare videre på \( z \)-komponenten. $$ \begin{align} \mathbf{E} &= \int_{x=-L}^L \frac{z\rho_l \d x}{4\pi\epsilon_0 (x^2+z^2)^\frac{3}{2}}\z \tag{5.23}\\ &= \frac{\rho_l z\z}{4\pi\epsilon_0} \left[ \frac{x}{z^2 \sqrt{x^2+z^2}}\right]_{-L}^L \z \tag{5.24}\\  &= \frac{L\rho_l}{2\pi\epsilon_0 z \sqrt{z^2+L^2}}\z \tag{5.25}\\ &= \frac{Q}{4\pi\epsilon_0 z \sqrt{z^2+L^2}} \tag{5.26} \end{align} $$ Der vi i den siste likheten har skrevet \( Q = 2L\rho_l \) der \( Q \) er stavens totale ladning. Selve integralet løser vi enten ved å bruke sympy/wolframalpha, eller på egenhånd med integrasjonsteknikker. I dette integralet fører det fram å gjøre to substitusjoner etter hverandre: \( u = \frac{x}{z} \) og \( u = \tan\theta \). Da vil vi ende opp med \( \int \cos\theta \d \theta = \sin\theta + C \), og innsatt for hva \( \sin\theta \) er for noe, får vi løsningen.

Når \( z \gg L \) vil \( z \) dominere over \( L \) inne i rottegnet slik at \( z\sqrt{z^2+L^2}\approx z^2 \). Dermed blir feltet for \( z \gg L \) $$ \begin{equation} \mathbf{E} \approx \frac{Q}{4\pi\epsilon_0 z^2}\z \tag{5.27} \end{equation} $$ som er det samme som feltet fra en punktladning. Dette gir mening, siden staven ser mer og mer ut som et punkt jo lenger unna man er.

Vi tar grenseverdien $$ \begin{align} &\lim_{L\to\infty} \frac{L}{\sqrt{z^2+L^2}} \tag{5.28}\\ &= \lim_{L\to\infty} \frac{L}{L\sqrt{\frac{z^2}{L^2}+1}} \tag{5.29}\\ &= \lim_{L\to\infty} \frac{1}{\sqrt{\frac{z^2}{L^2}+1}} \tag{5.30}\\ &= 1 \tag{5.31} \end{align} $$ slik at feltet i grensen der \( L\to\infty \) blir $$ \begin{equation} \mathbf{E} = \frac{\rho_l}{2\pi\epsilon_0 z} \z \tag{5.32} \end{equation} $$ Da vi to grenseverdien så vi at det avgjørende var å få \( \frac{z^2}{L^2} \) til å bli liten, så dette uttrykket er gyldig dersom man er veldig nærme staven sammenlignet med stavens lengde. Altså \( z \ll L \).

Use Laplace's equation.

Laplace's equation is given by \( \nabla^2 V = 0 \) (recall that we assume there's no free charges inside the trap, so \( \rho = 0 \)). $$ \begin{equation} \nabla^2 V = \frac{\partial^2 V}{\partial x^2} + \frac{\partial^2 V}{\partial y^2} + \frac{\partial^2 V}{\partial z^2} = 6A \neq 0. \tag{5.34} \end{equation} $$ Since \( V \) does not obey Laplace's equation, it's an unphysical electric potential and cannot exist in a vacuum.

Again, use Laplace's equation.

\( \beta = \alpha \) and \( \gamma = -2\alpha \)

The potential must obey Laplace's equation, so $$ \begin{equation} \nabla^2 V =2A(\alpha + \beta + \gamma ) = 0, \tag{5.37} \end{equation} $$ which can be achieved if \( \beta = \alpha \) and \( \gamma = -2\alpha \) (there are several other valid constraints, but these will be more convenient with respect to the geometrical setup of the trap). Setting \( \alpha = 1 \), we get $$ \begin{equation} V(x,y,z) = A(x^2 + y^2 - 2z^2). \tag{5.38} \end{equation} $$

The ring is held at a negative potential \( -V_0 \), so \( V(r_0, 0) = -V_0 \) which implies $$ \begin{equation} V(r_0, 0) = Ar_0^2 = -V_0 \implies A = -\frac{V_0}{r_0^2} \; . \tag{5.41} \end{equation} $$ The end caps is held at a positive potential \( V_0 \), so \( V(0,z_0) = V_0 \), giving $$ \begin{equation} V(0, z_0) = \frac{V_0}{r_0^2}(2z_0^2) = V_0 \; , \tag{5.42} \end{equation} $$ meaning \( r_0^2 = 2z_0^2 \). Clearly, then, the potential can be written as $$ \begin{equation} V(r,z) = \frac{V_0}{r_0^2}(2z^2 - r^2) \; . \label{} \end{equation} $$

You may do this in two ways: You can use a mathematical criterion in the form of the generalized second derivative test, the Hessian determinant, or you can plot the surface \( V(r,z) \) and use the surface plot to explain why you cannot trap the ion in this potential. You may need to reflect on how a potential needs to look in order to trap an ion.

The following Python program plots the potential \( V(r,z) \) as a surface or as a contour plot.

from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import numpy as np
z0 = 1
r0 = np.sqrt(2)*z0
r = np.linspace(0, r0, 1001)
z = np.linspace(-z0, z0, 1001)
r,z = np.meshgrid(r,z)
V = 2*z*z - r*r
# Plot a surface
fig = plt.figure()
ax = fig.gca(projection="3d")
surf = ax.plot_surface(r,z,V)
plt.show()
# Plot a contour plot
plt.contourf(r,z,V)
plt.colorbar()

To interpret the contour plot, it may be useful to remember that the gradient \( \nabla V \) in cylindrical coordinates is $$ \begin{equation} \nabla V(r,\phi,z) = \frac{\partial V}{\partial r}\rhat + \frac{1}{r}\frac{\partial V}{\partial \phi} \phihat + \frac{\partial V}{\partial z}\z \; , \tag{5.43} \end{equation} $$ and that \( V(r,z) \) does not have any \( \phi \)-dependence.

The Hessian matrix is given by $$ \begin{equation} H = \begin{bmatrix} \frac{\partial^2 V}{\partial r^2} & \frac{\partial^2 V}{\partial r \partial z} \\ \frac{\partial^2 V}{\partial r \partial z} & \frac{\partial^2 V}{\partial z^2} \end{bmatrix} = \begin{bmatrix} -\frac{2V_0}{r_0^2} & 0 \\ 0 & \frac{4V_0}{r_0^2} \end{bmatrix} \tag{5.44} \end{equation} $$ which has the determinant \( \det H = -8V_0^2/r_0^4 < 0 \). Since \( \det H < 0 \), there exists no stable equilibrium for the potential and thus we can't possibly trap the ion.

The code below was used to produce the plot. In the figure, we can see that there's no stable equilibrium points since there are no local minima. But then we can't hope to successfully trap the particle since there's no point in space the particle will oscillate about.

from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import numpy as np
fig = plt.figure()
ax = fig.gca(projection="3d")
z0 = 1
r0 = np.sqrt(2)*z0
r = np.linspace(0, r0, 1001)
z = np.linspace(-z0, z0, 1001)
r,z = np.meshgrid(r,z)
V = 2*z*z - r*r
surf = ax.plot_surface(r,z,V)
plt.show()

We find the force from \( \vec{F} = q\vec{E} \), where \( \vec{E} = - \nabla V \). We see that : $$ \begin{equation} \frac{\partial V}{\partial x} = \frac{V^2}{r_0^2} (-x) \; , \; \frac{\partial V}{\partial y} = \frac{V^2}{r_0^2} (-y) \; , \; \frac{\partial V}{\partial z} = \frac{V^2}{r_0^2} (2z) \; , \tag{5.46} \end{equation} $$ which gives $$ \begin{equation} \vec{E} = - \nabla V = - \left(\frac{\partial V}{\partial x}, \frac{\partial V}{\partial y}, \frac{\partial V}{\partial z}\right) = \frac{V^2}{r_0^2}\left( x,y,-2z \right) \; , \tag{5.47} \end{equation} $$ and $$ \begin{equation} \vec{F} = q \vec{E} = \frac{qV^2}{r_0^2}\left( x,y,-2z \right) \; . \tag{5.48} \end{equation} $$

You can make a contour plot of \( V(r,z) \) with the following program:

import numpy as np
import matplotlib.pyplot as plt
z0 = 1
rs = np.linspace(0,4*z0,1001)
zs = np.linspace(-z0, z0, 1001)
rs,zs = np.meshgrid(rs,zs)
Vs = 2*zs*zs-rs*rs
plt.contourf(rs,zs,Vs)
plt.colorbar()

To interpret the contour plot, it may be useful to remember that the gradient \( \nabla V \) in cylindrical coordinates is $$ \begin{equation} \nabla V(r,\phi,z) = \frac{\partial V}{\partial r}\rhat + \frac{1}{r}\frac{\partial V}{\partial \phi} \phihat + \frac{\partial V}{\partial z}\z \; , \tag{5.49} \end{equation} $$ and that \( V(r,z) \) does not have any \( \phi \)-dependence.

We find the electric field from \( \vec{E} = - \nabla V \): $$ \begin{align} \vec{E} &=& -\nabla V \tag{5.52}\\ &=& \frac{2V_0}{r_0^2}\cos(\Omega t)(x\x + y\y - 2z\z ) \; . \tag{5.53} \end{align} $$

We find the force from \( \vec{F} = q \vec{E} \): $$ \begin {equation} \vec{F} = q\vec{E} = q\frac{2V_0}{r_0^2}\cos\left( \Omega t \right) \left(x\x + y\y - 2z\z \right) \; . \tag{5.54} \end{equation} $$

For this problem you should use \( V_0 = 4000 \) V, \( \Omega = 100\pi \) Hz (that's the angular frequency a wall outlet would give you). In a demonstration of this type of trap one usually traps small, charged particles such as cinnamon. The mass of a cinnamon grain is roughly \( m \approx 5\times 10^{-5} \, \text{kg} \). The average charge per unit mass of a trapped cinnamon particle is roughly \( q/m = 10^{-4} \, \text{C/kg} \). A reasonable size for the trap is \( z_0 \approx 0.005 \ \text{m} \).

The following program find the trajectories:

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

def particle_trajectory(Nsteps):
    g = np.array([0,0,-9.81])
    m = 5e-5 # mass of grain of cinnamon
    V0 = 4000 # V
    q_per_m = 1e-4 # C/kg
    q = m*q_per_m
    Omega = 2*np.pi*50 # Hz
    dt = 1e-5 # Timestep
    z0 = 0.005 # Typical size of trap
    r0 = np.sqrt(2)*z0
    
    # Initialize trajectory
    r = np.zeros((Nsteps,3))
    v = np.zeros((Nsteps,3))
    t = np.zeros(Nsteps)
    r[0,:] = np.random.uniform(-0.5*z0,0.5*z0,size=3)
    v[0,:] = 10*np.random.uniform(-0.5*z0,0.5*z0,size=3)
    # Simulate motion
    for i in range(Nsteps-1):
        a = 2*q*V0/(m*r0**2)*np.cos(Omega*t[i])*np.array([r[i,0],r[i,1],-2*r[i,2]])+g
        v[i+1,:] = v[i,:] + a*dt
        r[i+1,:] = r[i,:] + v[i+1,:]*dt
        t[i+1] = t[i] + dt
    return r,v,t,z0
# Plotting N trajectories
N = 10
fig = plt.figure()
ax = fig.gca(projection='3d')
for j in range(N):
    r,v,t,z0 = particle_trajectory(20000)
    r = r/z0
    ax.plot(r[:,0], r[:,1], r[:,2])

The following figure shows 10 trajectories, which all are restricted to the region of the trap.

Dette systemet er sylindersymmetrisk. Systemet blir det samme om vi roterer det eller om vi forskyver det langs \( z \)-aksen. Derfor kan ikke potensialet endre seg langs \( z \)-aksen eller med \( \phi \). Potensialet er derfor \( V = V(r) \) og Laplace likning blir da $$ \begin{equation} \frac{1}{r}\frac{\partial}{\partial r}\left(r \frac{\partial V}{\partial r} \right) = 0 \; . \tag{5.56} \end{equation} $$

Laplace likning er i dette tilfellet: $$ \begin{equation} \frac{1}{r}\frac{\partial}{\partial r}\left(r \frac{\partial V}{\partial r} \right) = 0 \; . \tag{5.57} \end{equation} $$ For \( r>0 \) skriver vi det om til: $$ \begin{equation} \frac{\partial}{\partial r}\left(r \frac{\partial V}{\partial r} \right) = 0 \; . \tag{5.58} \end{equation} $$ Siden den deriverte med hensyn på \( r \) er null, er uttrykket inne i parantesen til venstre en konstant som vi kaller \( C_0 \): $$ \begin{equation} r \frac{\partial V}{\partial r} = C_0 \quad \Rightarrow \quad \frac{\partial V}{\partial r} = \frac{C_0}{r} \; . \tag{5.59} \end{equation} $$ Løsningen på denne likning kjenner vi igjen som logaritmen: $$ \begin{equation} V(r) = C_0 \ln r + C_1 \; , \tag{5.60} \end{equation} $$ hvor \( C_1 \) også er en konstant. Vi bestmmer \( C_0 \) og \( C_1 \) fra grensebetingelsene \( V(a) = V_0 \) og \( V(b) = 0 \). Vi begynner med \( V(b) = 0 \) som gir at \( C_0 \ln b + C_1 = 0 \) og dermed \( C_1 = - C_0 \ln b \) slik at \( V(r) = C_0 \ln r - C_0 \ln b = C_0 ( \ln r - \ln b) \). Vi setter dette inn i \( V(a) = V_0 = C_0 ( \ln a - \ln b) = C_0 \ln (a/b) \), slik at \( C_0 = V_0/\ln (a/b) \). Dermed blir løsningen $$ \begin{equation} V(r) = \frac{V_0}{\ln (a/b)} \left( \ln r - \ln b \right) \; . \tag{5.61} \end{equation} $$