Uke 11: Induktans
Læringsmål
Denne uken fokuserer vi på induktans, gjensidig induktans og anvendelser på transformatorer, og energi og energi-tetthet for magnetiske systemer.Diskusjonsoppgaver for gruppene
Exercise 12.1: Induktans
En tett spunnet toroide er en av noe få konfigurasjoner hvor det er enkelt å regne ut selvinduktansen. Hvilke egenskaper ved en toroide er det som gjør det enkelt?
Exercise 12.2: Energitetthet i magnetiserbare materialer
For den samme magnetiske feltstyrken, \( B \), er energitettheten høyere i vakuum eller i et magnetisk materiale? Forklar? Betyr likningen \( u = (1/2) B H \) at for en long solenoide med strømmen \( I \) så er den lagrede energien proporsjonal med \( 1/\mu \)? Og betyr dette at for den samme strømmen er det mindre energi lagret når solenoiden er fylt med et ferromagnetisk materiale i stedet for luft? Forklar.
Exercise 12.3: Energi i en spole
Først kobler du en spole til et batteri. Hvor mye energi er det i en spole med induktans \( L \) hvis det går en strøm \( I \) gjennom den? Du kobler hurtig av ledningen til batteriet slik at strømmen blir null. Hvor ble det av energien i spolen?
Gruppeoppgaver
Exercise 12.4: Self-inductance
In this tutorial we will focus on the strategy and procedure used to find the self-inductance \( L \) of a component. The strategy is similar to the strategies we have used to find the resistance and the capacitance of a component. The general strategy is that (1) we assume that a current \( I \) runs through the component, (2) we find the magnetic field \( \vec{B} \) due to this current, (3) we find the flux \( \Phi \) of this magnetic field through the curve \( C \) with the current \( I \), and (4) we find the self-inductance \( L = \Phi / I \).
We will address a long cylindrical solenoid of length \( h \), radius \( R \) and \( N \) turns of the wire.
a) Make a sketch of the solenoid as seen from above and from the side. Mark the direction of the current \( I \) through the solenoid in each of the drawings.
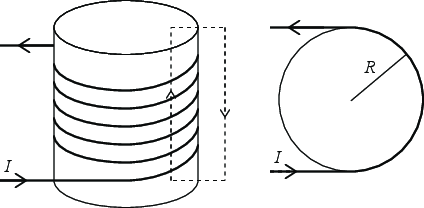
b) Assume that a current \( I \) runs through the wire. Use Amperes law for a well-chosen path to find the magnetic field \( \vec{B} \) inside the solenoid. (You can assume that the magnetic field \( \vec{B} \) is zero outside the solenoid). The field is a vector and should have a magnitude and a direction!
For the path shown in the figure above, Ampere's law gives $$ \begin{equation} \oint_C \vec{B} \cdot d \vec{l} = \mu_i I N \; , \tag{12.1} \end{equation} $$ where we have included \( I N \) as the total current going through the surface enclosed by the path \( C \). Along this path we see from symmetry that \( B \) has the same direction, and is directed along the integration path. It is only the path inside the solenoid that contributes. The integral is therefore \( Bh \), and $$ \begin{equation} Bh = \mu_0 N I \, \Rightarrow \, B = \frac{\mu_0 N I}{h} \; . \tag{12.2} \end{equation} $$
c) Find the flux of the magnetic field \( \vec{B} \) through the loop(s) of the wire. We recall that there are \( N \) loops of the wire, hence the relevant area is \( N \pi R^2 \):
The flux is given as $$ \begin{equation} \Phi = \int_S \vec{B} \cdot d \vec{S} = B \int_S dS = B \pi R^2 \, \Rightarrow \, \frac{mu_0 I \pi R^2 N^2}{h} \; . \tag{12.3} \end{equation} $$
d) Show that the self-inductance is \( L = \frac{\mu_0 \pi R^2 N^2}{h} \).
The self-inductance is then \( L = \Phi/I \). We insert the result from above for \( \Phi \) and find the result.
Exercise 12.5: Mutual inductance in a solenoid and a circular circuit
A solenoid consists of a wire wrapped \( N \) times around a cylinder of length \( L \) and radius \( a \). A circular circuit of radius \( b \) is centered on the cylinder as illustrated in Fig. 28.
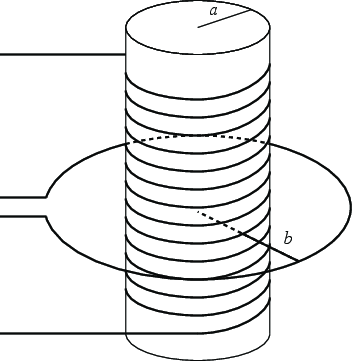 |
Figure 28: Two coupled circuits. |
a) What strategy would you choose to find the mutual inductance for this system? What symmetries would you use and how would you reason? In which system will you assume there is a current and in which system would you calculate the flux? Explain.
When we calculate the mutual inductance, we first want to find the circuit for which it is most simple to find the magnetic field. In this case, this is the solenoid. For this system, we can use the cylindrical symmetry to find the \( \vec{B} \)-field inside the solenoid. Outside the solenoid the field will be zero. We will therefore assume that there is a current \( I_1 \) in this system.
b) Based on your assumption, assume a current \( I_1 \) runs through your selected circuit 1. What is the magnetic field \( \vec{B}_1 \)? Explain the steps in the argument used to find \( \vec{B}_1 \). How does the argument depend on what is inside the solenoid?
We find the magnetic field by using Ampere's law for a path along the solenoid, first inside, then outside. For this path, the total current will be \( NI_1 \). The field inside will therefore be \( H_1 L = N I_1 \), that is \( H_1 = N I_1/L \) and \( B_1 = \mu H_1 = \mu N I_1/L \). The field outside is zero.
c) Given the magnetic field \( \vec{B}_1 \), what is the flux \( \Phi_{1,2} \) of \( \vec{B}_1 \) through circuit 2? Explain your reasoning.
The field is constant along the cross section of radius \( a \) and zero outside. Hence the flux is \( \Phi_{12} = B_1 \pi a^2 = \mu N I_1 \pi a^2 / L \).
d) Finally, find the mutual inductance \( L_{12} \) for this system.
\( L_{12} = \Phi_{12}/I_1 = \mu N \pi a^2/L \)
e) Can you extend your argument to the case where \( N=1 \) and \( b\gg a \)?
This corresponds to the case where the field is set up by a very small circuit. However, in this case, we cannot generally assume that the magnetic field is constant inside the circuit, but we may approximate the field with the value at the center of the circuit.
Exercise 12.6: Energy densities
A solenoid consists of a wire wrapped \( N \) times around a cylinder of length \( h \) and radius \( a \).
a) What is the magnetic fields \( \vec{H} \) and \( \vec{B} \) inside the solenoid when a current \( I \) is runnding through the wire?
\( \vec{H} = NI/h \hat{z} \), \( \vec{B} = \mu \vec{H} \).
\( \vec{H} = NI/h \hat{z} \), \( \vec{B} = \mu \vec{H} \).
b) What is the energy density inside the solenoid? And outside the solenoid?
\( u = (1/2) \vec{B}\cdot \vec{H} = (1/2) \mu (NI/h)^2 \)
\( u = (1/2) \vec{B}\cdot \vec{H} = (1/2) \mu (NI/h)^2 \)
c) What is the total energy stored in the solenoid when a current \( I \) is running through the wire?
\( W_m = u V = u \pi a^2 h = (1/2) \mu \pi a^2 (NI)^2/h \)
\( W_m = u V = u \pi a^2 h = (1/2) \mu \pi a^2 (NI)^2/h \)
d) Express the total energy in terms of the inductance \( L \) of the solenoid.
\( L = \Phi/I = N\pi a^2 \, \mu N/h \), \( W_m = (1/2) L I^2. \)
We find \( L \) to be \( L = \Phi/I = N\pi a^2 \, \mu N/h \) and that \( W_m = (1/2) L I^2. \)
Innleveringsoppgave (2 poeng)
Exercise 12.7: To sirkler
To sirkulære kretser er flettet inn i hverandre. En sirkel med radius \( a \) ligger i \( xy \)-planet med sentrum i origo.
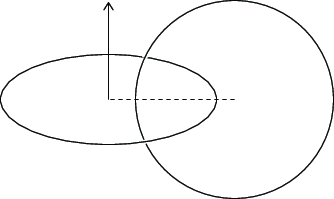
a) En annen sirkel med radius \( a \) ligger i \( xz \)-planet med sentrum i \( (b,0,0) \), hvor \( b>a \), som vist i figuren. Hva er den gjensidige induktansen, \( L_{12} \) til dette systemet?
\( L_{12} = 0 \) fordi magnetfeltet i \( xz \)-planet ikke har en komponent i \( y \)-retningen av symmetrigrunner.
Anta nå at den andre sirkelen i stedet ligger parallelt med \( xy \)-planet. Du kan anta at sirkelens sentrum er i \( (0,0,b) \) og at sirkelens radius \( R \) er svært liten sammenliknet med \( a \).
b) Finn et estimat for den gjensidige induktansen \( L_{12} \) til dette systemet. Begrunn kort hvilke tilnærminger du gjør.
Sirkelen med sentrum i \( (0,0,b) \) er så liten at du kan anta at det magnetiske feltet er homogent gjennom denne sirkelen.
Vi antar at magnetfelter er homogent over den lille sirkelen slik at fluksen gjennom denne er lik \( z \)-komponenten av magnetfeltet i midten av sirkelen ganget med arealet til sirkelen.
Vi har tidligere funnet \( z \)-komponenten til magnetfeltet langs \( z \)-aksen for dette systemet. Du kan finne dette utregnet i læreboken. Svaret er $$ \begin{equation*} B_z = \frac{\mu_0 I_1 a^2}{2 \left( z^2 + a^2 \right)^{3/2}} \; , \end{equation*} $$ hvor \( I_1 \) er strømmen som går gjennom kretsen. Fluksen gjennom krets 2 med radius \( R \) blir derfor \( \Phi = B_z \pi R^2 \) og dermed er den gjensidige induktansen, \( L_{12} = \Phi/I_1 \) lik: $$ \begin{equation*} L_{12} = \frac{\mu_0 a^2}{2 \left( z^2 + a^2 \right)^{3/2}} \, \pi R^2 \; . \end{equation*} $$
Eksamenstrening: Hvis du ønsker litt ekstra eksamenstrening kan du gjøre følgende frivillige ekstraoppgave til denne oppgaven:
Anta nå at den andre sirkelen ligger i \( xy \)-planet med sentrum i punktet \( (b,0,0) \). Du kan fremdeles anta at sirkelens radius \( R \) er svært liten sammenliknet med \( a \). Du kan i det følgende ta utgangspunkt i et program som finner det magnetiske feltet i et punkt \( \vec{r} \) fra en sirkulær krets med sentrum i origo og radius \( a \):
import numpy as np
import matplotlib.pyplot as plt
def bfieldlist(r,list):
# Find the magnetic field in the point r
# list = array(N,3) of points
B = np.array([0,0,0])
N = np.shape(list)[0]
for i in range(N):
i0 = i
i1 = i + 1
if (i1>N-1):
i1 = 0
rdv = 0.5*(list[i1,:]+list[i0,:])
R = r - rdv
dlv = list[i1,:]-list[i0,:]
dB = np.cross(dlv,R)/np.linalg.norm(R)**3
B = B + dB
return B
# Setup list of point for a circle
N = 25
a = 1
list = np.zeros((N,3),float)
dtheta = 2*np.pi/N
dl = a*dtheta
for i in range(N):
theta = i*dtheta
rdv = np.array([a*np.cos(theta),a*np.sin(theta),0])
list[i,:] = rdv
# Finding the magnetic field in the origin
Bx,By,Bz = bfieldlist(np.array([0,0,0]),list)
c) Finn den gjensidige induktansen \( L_{12}(b) \) som funksjon av \( b \) og lag et plot som viser oppførselen.
Vi finner den gjensidige induktansen langs en linje langs \( x \)-aksen ved
bi = np.linspace(0,4,1000)
Bzi = bi.copy()
for i in range(len(bi)):
r = np.array([bi[i],0,0])
Bx,By,Bz = bfieldlist(r,list)
Bzi[i] = Bz
plt.plot(xi,Bzi)
d) Studer hva som skjer når \( b\rightarrow a \) ved å endre på parametere i modellen og i den numeriske tilnærmingen, slik som å endre på antall elementer som brukes til å representere strømkretsen. Reflekter kort omkring tilnærmingene som du gjør og modellen.