Uke 06: Strøm, motstand og enkle kretser
Læringsmål
Vi beskriver strøm av ladninger ved hjelp av strømtettheten \( \vec{J} \), Ohms lov på differensiell form, \( \vec{J} = \sigma \vec{E} \) og ladningsbevaring, \( \nabla \cdot \vec{J} = - \partial \rho/\partial t \) og bruker det vi kan til å finne resistansen til en motstand for forskjellige motstandsgeometrier. Det er spesielt viktig å lære seg hvordan vi ofte tar utgangspunkt i strømtettheten og bruker dette til å finne det elektriske feltet med Ohms lov når vi skal finne resistansen til en komponent.(AMS 10: Learning outcomes for this tutorial: (1) Understand and use the current density and Ohm's law to find the resistance of a system. Here we will do this in a structured way for a simple system. (2) Use conservation of charge and Kirchoff's laws. Here we will use this to address flow through various cross sections of a conductor, and we will use this to address properties of current densities \( \vec{J}(\vec{r}) \).)
Test-deg-selv oppgaver
(Disse oppgavene kan du se på før gruppene for å forberede deg til aktiviteten på gruppene.)
Exercise 7.1: Current of ions
Positive ions flow to the right through a liquid, negative ions flow to the left. The spatial density and velocity of both types of ions are identical. Is there a net current through the liquid?
Yes, to the right.
Diskusjonsoppgaver for gruppene
Exercise 7.2: Strømtetthet og strøm
Du har en lang stav med kvadratisk tverrsnitt og det går en strøm med homogen strømtetthet rettet langsmed staven. Er strømmen gjennom flaten \( S_1 \) den samme som gjennom flaten \( S_2 \)?
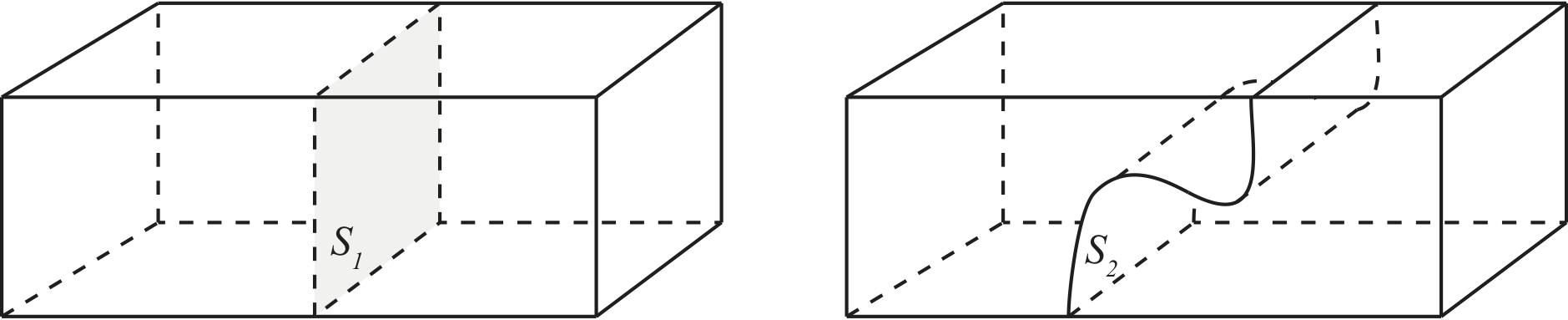
Exercise 7.3: Ladningsoppsamling
Er netto strøm av ladning ut av en lukket overflate alltid null? Hvis ikke, kan du komme med noen moteksempler?
Gruppeoppgaver
Exercise 7.4: Current density
(AMS 11: Concept and practice)
a) For a homogeneous current density \( \vec{J} = J_0 \hat{x} \), what is the current through all the surfaces of a cube with corners at \( (-1,-1,-1) \), \( (-1,+1,-1) \), \( (+1,-1,-1) \), \( (+1,+1,-1) \), \( (-1,-1,+1) \), \( (-1,+1,+1) \), \( (+1,-1,+1) \), and \( (+1,+1,+1) \) all measured in units of \( a \).
\( I=\pm J_0 4 a^2 \) for the surfaces through \( (\pm1,0,0) \), and zero for the other surfaces.
We notice that the area of the each of the squares are \( 4 a^2 \). The current is \( I = \vec{J} \cdot \vec{S} \). It is only the surfaces with normals in the \( \hat{x} \) direction that will have non-zero currents. For the surface through \( (1,0,0) \) the current is \( 4 a^2 J_0 \) since the surface normal is in the positive \( x \)-direction, and for the surface through \( (-1,0,0) \) the current is \( -4 a^2 J_0 \) since the surface normal is in the negative \( x \)-direction.
b) A block with uniform charge density \( \rho \) is moving with a constant velocity \( \vec{v} = v_0\hat{z} \). What is the current density \( \vec{J} \) at a specific point in space inside the block (the point does not move along with the block). What would the current density \( \vec{J} \) be if the point moved along with the block?
\( \vec{J} = \rho v_0 \hat{z} \).
The current density will be in the direction of \( \vec{v} \). The amount of charge moving through a small surface \( S \) with a normal in the \( \hat{z} \) direction in a time interval \( dt \) will be \( dq = \rho dV = \rho S v_0 dt \), thus \( I = dq/dt = \rho S v_0 \) and the current density will be \( \vec{J} = \rho v_0 \hat{z} \).
Exercise 7.5: Cylindrical resistor
We will now look at charges that are leaking across the cylindrical membrane of a part of the axon of length \( L \). We will assume that the myelin sheath is leaky (a conductor with conductivity \( \sigma \)) and that there is a radially-symmetric current density \( \vec{J} \) leaking across it due to a potential difference. We will find the resistance \( R \) of a piece of the cylinder of length \( L \). We assuming that the inner part of the cylidrical shell is connected to a potential \( V \) and that the outer part of the shell is connected to a potential \( V=0 \).
We will find the resitance of this system by (i) making a drawing of the system, (ii) drawing the expected current density, (iii) finding the electric field for this current density, (iv) finding the potential by integrating the electric field, and (v) finding the resistance by relating the current to the potential difference. (Notice the similarity of this method and the method you used to find the capacitance!)
a) Make a drawing of the cylindrical system. Sketch the current density.
b) Given that there is a radially-symmetric current density, find the current density \( \vec{J} \) expressed in terms of the total current \( I \).
Integrate the current density along a cylindrical surface.
We find the current density, by realizing that the current must be the same through each cylindrical surface with radius \( r \) --- due to symmetry. The current \( I \) is therefore found from the surface integral of \( \vec{J} \) over the cylindrical surface \( S \): $$ \begin{equation} I = \int_S \vec{J} \cdot d \vec{S} = 2 \pi r L J \, \Rightarrow \, J = I/(2 \pi r L) \; . \tag{7.1} \end{equation} $$ This is only valid for \( a < r < b \), otherwise the current density is zero.
c) Find the electric field \( \vec{E} \) by using the current-density version of Ohm's law.
\( \vec{E} = I/(2 \pi r L \sigma) \, \hat{r} \) when \( a < r < b \) and \( 0 \) otherwise.
The plan is to find the electric field by first finding the electric current density \( \vec{J} \) and then finding the electric field from the current density using Ohm's law, \( \vec{E} = (1/\sigma) \vec{J} \). Based on the current density we found above, we can use Ohm's law to find: $$ \begin{equation} \vec{E} = \frac{1}{\sigma} \vec{J} = \frac{I}{2 \pi r L \sigma}\hat{r} \; , \tag{7.2} \end{equation} $$ when \( a < r < b \), otherwise \( \vec{E} = 0 \).
d) Use the electric field to relate the current \( I \) to the voltage difference between the inner \( V(r=a) \) and outer \( V(r=b)=0 \) surfaces of the axon.
\( V = I/(2 \pi L \sigma) \, \ln (b/a) \)
We find the potential by integrating the electric field from \( r=a \) to \( r=b \) where \( V(b)=0 \): $$ \begin{equation} V(a)-V(b) = V(a)-0=V(a) = \int_{a}^{b} \frac{I}{2 \pi r L \sigma}dr = \frac{I}{2 \pi L \sigma} \ln (b/a) \; . \tag{7.3} \end{equation} $$
e) Find the resistance of the cylinderical shell. Is this the resistance for flow along the axon?
\( R = \ln(b/a)/(2 \pi L \sigma) \)
The resistance is found from \( R=V/I \), giving $$ \begin{equation} R = \frac{V}{I} = \frac{I}{2 \pi L \sigma I} \ln (b/a) = \frac{\ln(b/a)}{2 \pi L \sigma} \tag{7.4} \end{equation} $$
f) Interpret these expressions. Does the current you found actually depend on the length of the axon? Does the resistance?
Hjemmeoppgaver
Exercise 7.6: Lightning
Lightning strikes in one end of a lightning rod of steel and induces a current of \( 30 000 \) A which lasts for \( 65\text{ }\mathrm{\mu}\text{s} \). The lightning rod is a \( 1 \) m long and \( 2 \) cm in diameter, and the other end is connected to the ground through a \( 40 \) m copper wire with a diameter of \( 5 \) mm. The conductivity of steel and copper is respectively \( \sigma_{\text{steel}} = 5.0\cdot 10^6 \mathrm{ \Omega}^{-1}\text{m}^{-1} \) og \( \sigma_{\text{copper}} = 5.8\cdot 10^7 \mathrm{ \Omega}^{-1}\text{m}^{-1} \).
a) Find the potential difference between the top of the lightning rod and the bottom of the copper wire as the current is passing through.
\( 1.1 \) kV
We know that \( V = RI \) where \( R = \frac{L}{A\sigma} \), \( L \) is the length of the conductor, \( A \) is the cross-sectional area, and \( \sigma \) is the conductivity. The two parts of the conductor are connected in series so that the resistances can be added: $$ \begin{eqnarray} R &=& \frac{L_\text{steel}}{A_\text{steel}\sigma_\text{steel}} + \frac{L_\text{copper}}{A_\text{copper}\sigma_\text{copper}} \\ &=& 0.036 \mathrm{\Omega} \end{eqnarray} $$
Ls = 1.0
As = pi*0.01**2
ss = 5e6
Lc = 40
Ac = pi*0.0025**2
sc = 5.8e7
Rs = Ls/(As*ss)
Rc = Lc/(Ac*sc)
R = Rs + Rc
print(R)
0.03576046928230311
Ohm's law states that \( V = RI \), so that the potential across the lightning rod is $$ \begin{equation} V = RI = 1072 \text{ V} \simeq 1.1 \text{ kV} \tag{7.5} \end{equation} $$
I = 30000
V = R*I
print(V)
1072.8140784690931
b) Find the total energy dissipated in the lightning rod and the copper wire from the lightning strike.
\( 2.1 \) kJ
The dissipated power is \( P = VI = RI^2 \), and dissipated energy at constant current over a given time \( t \) is $$ \begin{equation} E = Pt = RI^2 t = 2091 \text{ J} \tag{7.6} \end{equation} $$
t = 65e-6
P = R*I**2
E = P*t
print(E)
2091.9874530147317
Exercise 7.7: Sfærisk symmetrisk strøm
Vi skal nå se på to konsentriske kuleskall, laget av metall, med radius \( a \) og \( b \) der \( (a < b) \). I sjiktet mellom kuleskallene er det et svakt ledende materiale med konduktivitet \( \sigma \). Husk at konduktivitet er definert som \( \sigma \equiv1/\rho \), der \( \rho \) er resistiviteten til materialet.
a) Anta at ved tiden \( t=0 \) finnes det en ladning \( +Q \) på det innerste kuleskallet, og en ladning \( -Q \) på det ytterste skallet. Finn strømtettheten som funksjon av posisjon mellom kuleskallene, \( \vec J = \vec J(r). \)
Stømtetthet \( J=I/A \). Resistiviteten er definert som \( \rho=E/J \). Vi bruker Gauss lov til å finne det elektriske feltet mellom kuleskallene. Feltet er \( E(r) = \frac{Q}{4\pi\epsilon_0 r^2} \) for \( a < r < b \). Dermed er strømtettheten $$ \begin{equation} J(r) = E(r)/\rho = \sigma E(r) = \frac{\sigma Q}{4\pi\epsilon_0 r^2} \tag{7.7} \end{equation} $$
b) Finn strømmen \( I(t=0) \) fra det innerste kuleskallet til det ytterste.
Når vi kjenner strømtettheten over et kuleskall kan vi finne strømmen: $$ \begin{equation} I = JA = \frac{\sigma Q}{4\pi\epsilon_0 r^2} \times 4\pi r^2 = \frac{\sigma Q}{\epsilon_0} \tag{7.8} \end{equation} $$
c) Finn resistansen i materialet mellom kuleskallene.
Resistansen kan beregnes på flere måter. Her velger vi å integrere resistiviteten. $$ \begin{equation} R = \int_a^b \frac{\rho dr}{4\pi r^2} = -\frac{\rho}{4\pi} \left[\frac{1}{r} \right]_a^b = \frac{\rho}{4\pi} \left(\frac{1}{a} - \frac{1}{b} \right) = \frac{1}{4\pi\sigma} \left(\frac{1}{a} - \frac{1}{b} \right) \tag{7.9} \end{equation} $$
Exercise 7.8: Resistivitet i en konusformet leder
Vi har en konusformet (avkappet kjegle) leder med resistivitet \( \rho \). Radiene i endene er \( r_1 \) og \( r_2 \) og lengden er \( L \).
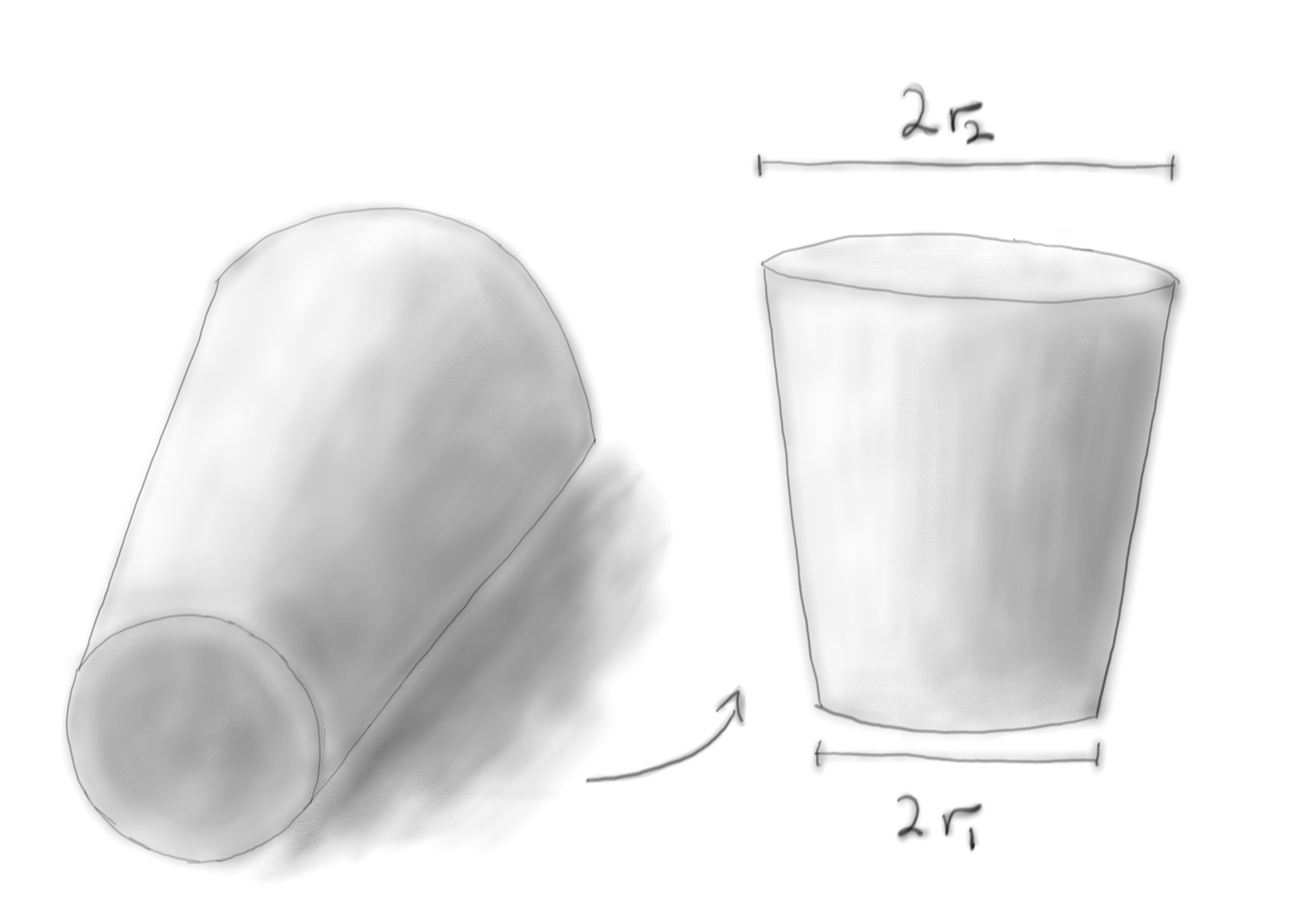
a) Beregn motstanden mellom endeflatene i lederen.
Vi begynner med å finne radien som funksjon av hvor på konusen vi er: $$ \begin{align} r(z) = r_1 + \frac{r_2 - r_1}{L} z \tag{7.11} \end{align} $$
Videre ønsker vi å finne motstanden ved å integrere opp infinitesimale sylindere med høyde \( \d z \), siden vi vet at motstanden i en sylinder er \( \frac{\rho}{\pi r^2}h \). $$ \begin{align} R = \int_{z=0}^L \frac{\rho}{\pi r^2} \d z \tag{7.12}\\ &= \int_{r = r_1}^{r_2} \frac{\rho}{\pi r^2}\frac{L}{r_2-r_1} \d r \tag{7.13}\\ &= \frac{\rho L}{\pi (r_2-r_1)} \left[-\frac{1}{r}\right]_{r = r_1}^{r_2} \tag{7.14}\\ &= \frac{\rho L}{\pi r_1 r_2} \tag{7.15} \end{align} $$
b) Sjekk at resultatet ditt er konsistent med motstanden i en sylinderformet leder: \( R = \rho L / \pi r^2 \).
Vi setter inn for \( r_1 = r_2 = r \), og får $$ \begin{equation} R = \frac{\rho L}{\pi r^2} \tag{7.16} \end{equation} $$ Som er uttrykket for motstanden i en sylinderformet leder.
c) På en eller annen måte klarer vi å gi konusen en strømtetthet på \( |\mathbf{J}| = a r \) rettet langs konusaksen. Finn forskjellen i strøm fra den ene enden til den andre. Vil denne lederen forbli nøytral over tid?
\( \Delta I_{r_2-r_1} = a\pi (r_2^3 - r_1^3) \). Nei.
Siden strøm er endring i ladning per tid, og denne endringa ikke er lik over alt i lederen, så vil det hope seg opp med ladning. Lederen vil ikke forbli nøytral over tid.
Exercise 7.9: Leaky coaxial cable
A 10 km long coaxial cable lies on the ocean floor. The internal radius is \( a = 15 \) mm, and the external is \( b = 30 \) mm as in Fig. 17. The cable itself is made of a superconductor, and the voltage carried by the cable is \( V_0 = 520 \) V.
 |
Figure 17: Illustration of a coaxial cable. |
a) What is the current density \( \vec{J} \) inside the cable?
\( \vec{J} = \frac{\sigma V_0}{r \ln \frac{b}{a}}\rhat \)
We use Gauss' law on a cylinder of length \( L \) and radius \( a < r < b \) inside the coax cable. Due to cylindrical symmetry we get $$ \begin{equation*} \vec{E} = \frac{\rho}{2 \pi \epsilon r}\rhat \; , \end{equation*} $$ where \( \rho \) is the charge density per unit length in the cable. As the value of \( V_0 \) is known, we can eliminate \( \rho \) from the above by calculating $$ \begin{eqnarray*} V_0 &=& \int_a^b \vec{E}\cdot \d\vec{l} = \int_a^b Edr = \frac{\rho}{2 \pi\epsilon}\int_a^b\frac{1}{r} \d r = \frac{\rho}{2 \pi\epsilon} \ln \frac{b}{a}\\ \Rightarrow \rho &=& \frac{2 \pi \epsilon V_0}{\ln \frac{b}{a}}. \end{eqnarray*} $$ Insert \( \rho \) into the equation for \( \vec{E} \) and apply Ohms law to get $$ \begin{equation} \vec{J} = \frac{\sigma V_0}{r \ln \frac{b}{a}}\rhat \; , \label{} \end{equation} $$ for \( a < r < b \).
b) At one point the cable gets a leak and the entire space between the conductors are filled with seawater (\( \sigma = 4 \Omega^{-1}\text{m}^{-1} \)).\\ How much power is lost to the seawater inside the cable?
\( P_J = 98 \) GW
We find the power loss by computing the following integral over the volume \( v \) (all of the space between the conductors in the cable): $$ \begin{eqnarray*} P_J &=& \int_v \vec{J}\cdot \vec{E} \d v \\ &=& \int_0^L\int_0^{2\pi}\int_a^b \frac{V_0^2 \sigma}{\left( \ln \frac{b}{a}\right)^2} \frac{1}{r^2} r \d r \d\phi\d z \\ &=& \frac{V_0^2 \sigma}{\left( \ln \frac{b}{a}\right) ^2}\left[ L\cdot 2\pi\cdot (\ln b - \ln a) \right] \\ &=& \frac{2\pi \sigma V_0^2 L}{\ln \frac{b}{a}}. \end{eqnarray*} $$ Insert the given values to get \( P_J = 98 \) GW.
c) There is a generator connected to one of the ends of the cable. When the cable is filled with water, what is the resistance seen by this generator? Comment on this value in regards to the value of \( P_J \).
\( R = 2.76 \mu \Omega \).
We have \( P_J = \frac{V_0^2}{R} \). Solve for \( R \) to get \( R = 2.76 \mu \Omega \).
The resistance is very small, which might lead one to think that the energy loss is minuscule. This is, however, not the case as the power loss due to the sea water is \( P_J = 98 \) GW. This goes to show that there are several factors, not just the magnitude of the resistance, involved in the size of the energy loss.
Innleveringsoppgave (2 poeng)
Exercise 7.10: Motstand av to sylindere
a) En motstand består av en sylinder med radius \( r_0 \), lengde \( L \) og konduktivitet \( \sigma \). Finn motstanden til sylinderen i lengderetningen.
Fordi sylinderen ikke overraskende er sylindersymmetrisk bruker vi sylinderkoordinater og legger sylinderen langs \( z \)-aksen. Vi antar at det går en strøm \( I \) gjennom sylinderen. Hvordan er denne fordelt i et tverrsnitt gjennom sylinderen? Fordi sylinderen er homogen, antar vi at strømtettheten er homogen, \( J_z = I/A = I/(\pi r_0^2) \). Ohms lov gir at at det elektriske feltet er \( E_z = J_z/\sigma = I/(\sigma \pi r_0^2) \). Spenningsforskjellen er da gitt som $$\Delta V = \int_0^L E_z \d z = \frac{I L }{\sigma \pi r_0^2} = \frac{L }{\sigma \pi r_0^2} I \; .$$ Og dermed er motstanden $$R = \frac{L }{\sigma \pi r_0^2} \; .$$
(Kommentar som ikke er en del av oppgaven: Merk at elektrisk strøm er ganske forskjellig fra f.eks. strøm av vann i et rør. For strøm av vann i et rør, henger vannet igjen på ytterkanten av røret og det er vannets motstand mot hastighetsforskjeller på tvers av strømningsretningen - kalt viskositet - som gjør at det blir en forskjell i strømtettheten på tvers av en et rør. Strøm av elektroner i en dårlig leder er mer som strøm gjennom et porøs materiale, hvor elektronene merker en motstand mot strømmen pga. vekselvirkninger med det underliggende materialet. Derfor er det ikke en hastighetsvarisjon på tvers av en elektrisk kabel - i alle fall ikke på grunn av denne effekten).
b) En motstand består av to sylindere. Den første har radius \( a \) og den andre har radius \( a/2 \). Begge har lengde \( L/2 \) og har konduktivitet \( \sigma \). Du kan anta sylindrene er skjøtet sammen med et tynt lag med en god leder. Finn motstanden til denne sylinderen i lengderetningen.
Denne oppgaven kan vi løse på (minst) to forskjellige måter om begge er fullgode: (i) bruke seriekoblinger av mostander, (ii) regne ut motstanden for den kombinerte komponenten.
Seriekopling: Siden motstandene er koblet sammen med en god leder, kan vi anta at de er koblet etter hverandre i serie. Den totale motstanden er da summen av motstanden. Motstanden til sylinderen med radius \( a \) og lengden \( L/2 \) er \( R_1 = \frac{L/2}{\sigma \pi a^2} = \frac{L}{2 \sigma \pi a^2} \). Motstanden til sylinderen med radius \( a/2 \) og lengden \( L/2 \) er \( R_2 = \frac{L}{2 \sigma \pi (a/2)^2} = \frac{2L}{\sigma \pi a^2} \). Til sammen blir motstanden til hele komponenten $$R = R_1 + R_2 = \frac{L}{2 \sigma \pi a^2} + \frac{2L}{\sigma \pi a^2} = \frac{5L}{2\sigma \pi a^2} \; .$$
Kombinert komponent: Du kan også løse oppgaven ved å finne det elektriske feltet i hver del av komponenten. Vi antar at det går en strøm \( I \) gjennom komponent. Den må være den samme i begge sylindrene, men strømtettheten blir forskjellig. I komponenten med radius \( a \) blir strømtettheten \( J_{1,z} = I/(\pi a^2) \), mens i komponenten med radius \( a/2 \) blir strømtettheten \( J_{2,z} = I/(\pi (a/2)^2)= 4I/(\pi a^2) \). Ohms lov for hver av de to sylindrene gir at \( E_{1,z} = J_{1,z}/\sigma \) og tilsvarende \( E_{2,z} = J_{2,z}/\sigma \). Spenningsfallet over hver av de to sylindrene finner vi ved å integrere det elektriske feltet over avstanden \( L/2 \), slik at \( V_1 = E_{1,z}L/2 \) og \( V_2 = E_{2,z}L/2 \) som gir hvor \( V_1 \) er spenningsfellet over sylinderen med radius \( a \) og \( V_2 \) er spenningsfallet over sylinderen med radius \( a/2 \). Det totale spenningsfallet blir $$V = V_1 + V_2 = \frac{I (L/2)}{\sigma \pi a^2}I/(\pi a^2) + \frac{4I (L/2)}{\sigma \pi a^2} = \frac{5 L}{2\sigma \pi a^2} \, I $$ Dette gir oss den samme motstanden i begge metodene - heldigvis!
c) En motstand består av 3 sylindere, hver med lengde \( L/3 \) og konduktivitet \( \sigma \). Den først har radius \( a \), den andre har radius \( 3a/4 \), og den tredje har radius \( 2a/4=a/2 \). Finn motstanden til denne sylinderen i lengderetningen.
Her kan vi bruke samme metoder som ovenfor. Vi velger å legge sammen motstander i serie. Hva blir motstandene? $$R_1 = \frac{(L/3)}{\sigma \pi a^2} = \frac{L}{3 \sigma \pi a^2}$$ $$R_2 = \frac{(L/3)}{\sigma \pi (3a/4)^2} = \frac{16 L}{27 \sigma \pi a^2}$$ $$R_3 = \frac{(L/3)}{\sigma \pi (a/2)^2} = \frac{4 L}{3 \sigma \pi a^2}$$ Summen av motstandene blir da: $$R = R_1 + R_2 + R_3 = \frac{L}{\sigma \pi a^2}\left( \frac{9}{27}+\frac{16}{27} + \frac{36}{27}\right) = \frac{L}{\sigma \pi a^2} \frac{61}{27} $$
d) I oppgave c, betyr rekkefølgen på sylindrene noe? Begrunn svaret. Hvis vi fortsetter oppdelingen i mindre og mindre biter etter mønster av det vi har gjort til nå, kan man få noe som likner på en konisk motstand. Synes du dette er en god modell for en konisk motstand? Begrunn svaret.
Nei, rekkefølgen betyr ikke noe, fordi rekkefølgen på leddene i summen for \( R \) kan stokkes fritt om. (Eller vi kan endre på rekkefølgene av komponentene). Det betyr at dette ikke er god modell for en konisk motstand. I en virkelig konisk motstand vil det også være komponenter av \( \vec{J} \) som ikke er parallel med aksen til sylinderen/konet, og det har vi ikke tatt hensyn til her.