Uke 09: Amperes lov og magnetiske materialer

Forelesning.

Metode: Magnetiske kretser

(Lærebok 12.3.1)

Eksempel.

Eksempel: Toroidal krets

(Lærebok 12.3.2)

Oppgave.

Oppgave: Flukser

Figuren viser en magnetisk krets som består av en sylindrisk toroide med ferromagnetisk materiale med en stor $ \mu_r $. Den venstre halvdelen har en radius $ a $ slik at tverrsnittet er $ S_a = \pi a^2 $. Den høyre halvdelen har en radius $ b $ slik at tverrsnittet er $ S_b = \pi b^2 $. Radius til toroiden er $ c $. Anta at magnetfeltet i tverrsnittet $ S_1 $ er $ B_1 $.

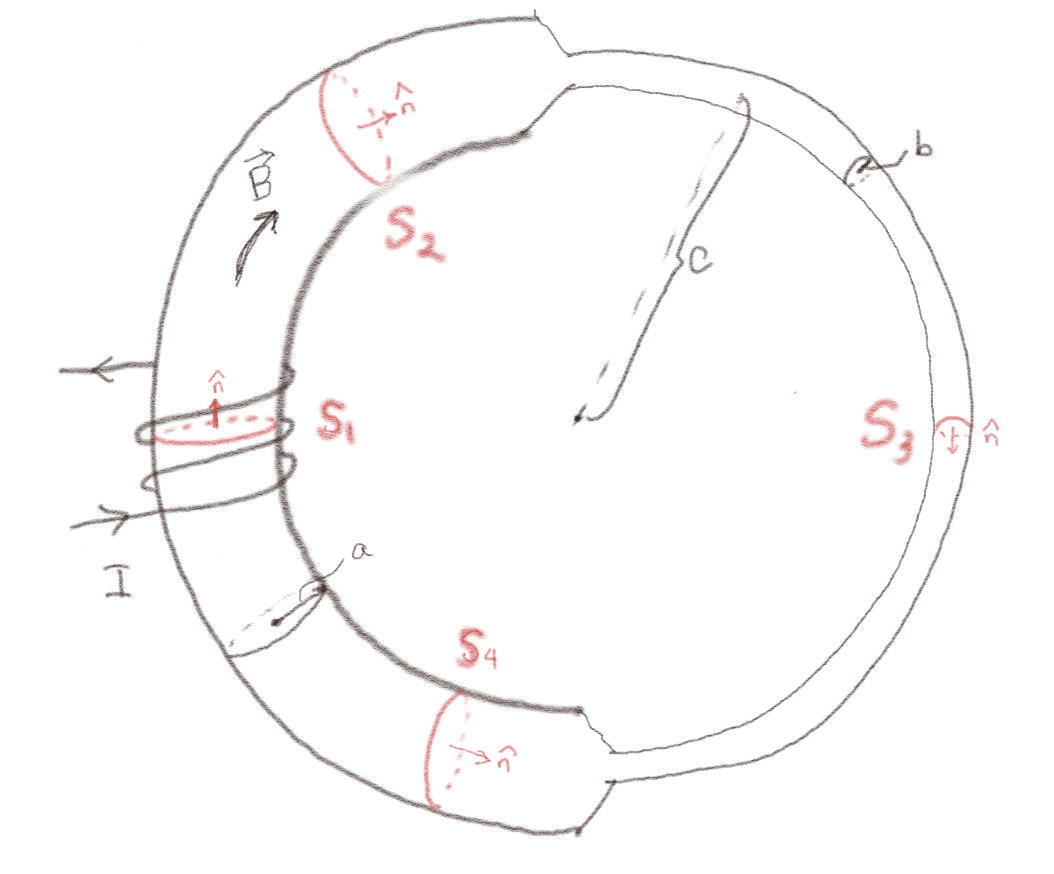
a) Hva er fluksen $ \Phi_{B,1} $ av magnetfeltet gjennom $ S_1 $?

Answer.

$ B_1 \pi a^2 $

Solution.

Vi antar at magnetfeltet er homogent over tverrsnittet. Fluksen er derfor $$ \begin{equation} \Phi_{B,1} = \int_{S_1} \vec{B} \cdot \nhat_1 \d S = B_1 \pi a^2 \; . \tag{26} \end{equation} $$

b) Hva er fluksen $ \Phi_{B,2} $ gjennom $ S_2 $?

Answer.

$ B_1 \pi a^2 $

Solution.

Fluksen er bevart langs kretsen. Den er derfor det samme som for $ S_1 $.

c) Hva er fluksen $ \Phi_{B,3} $ gjennom $ S_3 $?

Answer.

$ B_1 \pi a^2 $

Solution.

Fluksen er bevart langs kretsen. Den er derfor det samme som for $ S_1 $.

d) Hva er fluksen $ \Phi_{B,4} $ gjennom $ S_4 $?

Answer.

$ -B_1 \pi a^2 $

Solution.

Fluksen er bevart langs kretsen. Men her er flatenormalen tegnet i motsatt retning av $ \vec{B} $-feltet. Fluksen gjennom overflaten med denne orienteringen er derfor minus den tilsvarende overflaten men med motsatt rettet overflatenormalt. Fluksen er derfor minus fluksen ved $ S_1 $.

e) Hva er magnetfeltet $ B_3 $ i tverrsnittet $ S_3 $?

Answer.

$ B_3 = (a/b)^2 B_1 $.

Solution.

Siden fluksen er bevart og radius ved $ S_3 $ er $ b $ vil fluksen gjennom $ S_3 $ være $ \Phi_{B,3} = B_3 \pi b^2 $. Denne er det samme som gjennom $ S_1 $ hvor $ \Phi_{B,1} = B_1 \pi a^2 $ slik at $ B_3 \pi b^2 = B_1 \pi a^2 $ og $ B_3 = (a/b)^2 B_1 $.

Eksempel.

Eksempel: Varierende tverrsnitt og Kirchoffs lover

(Lærebok 12.3.3)