Oppgave
Oppgave: Selv-induktans per lengde
Vi ser på to tynne ledninger som henger i luften of fører en tidsvarierende strøm. Ledningene er tynne med radius \( a \) og de henger i en avstand \( d \) fra hverandre (\( d \) er avstanden mellom sentrum av ledningene). Vi tenker på dette som en lukket krets hvor det går en strøm \( I \) den ene veien i den ene ledningen og den andre veien i den andre ledningen. Vi antar at kretsen er lang, slik at vi kan se bort fra kant-effekter ved slutten av ledningen.
a) Plasser en ledning med sentrum i origio og den andre med sentrum i \( (d,0,0) \). La ledningen gå i \( y \)-retningen. Lag en tegning av systemet.
Figure 2
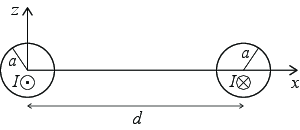
b) Finn magnetfeltet fra ledningen som ligger i origo som funksjon av \( x \).
$$B_z = \frac{\mu_0 I}{2 \pi x}$$
c) Finn magnetfeltet fra ledningen som ligger i \( (d,0,0) \) som funksjon av \( x \).
$$B_z = \frac{\mu_0 I}{2 \pi (d-x)}$$
d) Hvorfor tror du det ble spesifisert at ledningen hadde en endelig tykkelse \( a \)?
Fordi ellers vil magnetfeltet divergere i området vi skal beregne fluksen.
e) Finn fluksen av det totale magnetfeltet for en lengden \( \ell \) langsmed ledningene.
$$\Phi_B = \frac{\mu_0 I \ell}{\pi }\ln \frac{d-a}{a}$$
f) Finn induktansen per lengdeenhet for dette systemet.
$$L/\ell = \frac{\mu_0}{\pi }\ln \frac{d-a}{a}$$
g) Hvis vi ønsker liten induktans, hvordan bør i da konstruere et slikt system?