Seminar uke 02: Elektrisk potensial

Oppgave

Oppgave: Elektrisk potensial og potensiell energi

To plater er ladet slik at det er et uniform elektrisk felt $ \vec{E} = -E_0 \y $ mellom platene. Et proton med ladning $ Q = +e $ løftes med en ytre kraft (fra en optisk tweezer) en avstand $ d $ fra den nederste til den øverste platen. (Du kan se bort fra gravitasjonen på protonet i denne oppgaven).

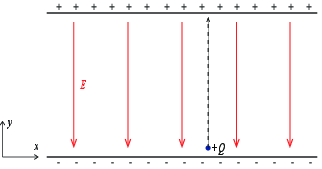
a) Hvilken retning har kraften på ladningen fra det elektriske feltet?

Answer.

Nedover, i negativ $ y $-retning.

b) Arbeidet som gjøres av det elektriske feltet er: (A) Positivt, (B) Negativt, (C) Null.

Answer.

Negativt

Solution.

Arbeidet er $$W = \int_0^d e \vec{E} \cdot \d \vec{l} = - e E_0 \y \cdot \int_0^d \y d \vec{l} = - e E_0 \y \cdot (d \y) = - e E_0 d$$ som er negativt.

c) Arbeidet som gjøres av den eksterne kraften (tweezer) er: (A) Positivt, (B) Negativt, (C) Null.

Answer.

Positivt

Solution.

Vi antar at tweezeren beveger ladning sakte, slik at summen av krefter er tilnærmet lik null gjennom hele bevegelsen. Da er kraften fra tweezeren motsatt rettet (har motsatt fortegn) av kraften fra feltet. Siden arbeidet som utføres av feltet er negativt, betyr det at arbeidet utført av tweezeren er positivt.

d) Endring i potensiell energi er definert som $ \Delta U = + W_{\text{ext}} = - W_{\text{felt}} $. Vi definerer den potensielle energien til protonet til å være $ U_p(y=0) = 0 $ nær den nedre platen. Hva er da $ U_p(y=d) $?

Answer.

$ U_p(y=d) = e E_0 d $

Solution.

Vi finner $$U(d) = \int_0^d \vec{F}_{\text{ext}} \cdot \d \vec{l} = \int_0^d - \vec{F} \cdot \d \vec{l} = \int_0^d-( - e E_0 \y) \cdot \d y \y = e E_0 d$$

e) Skisser det elektriske potensialet langs $ y $-aksen.

Answer.

$ V = E_0 y $

Solution.

Nullpunktet (referansepunktet) er ved $ y=0 $. Potensialet er da: $$V(y) = \int_y^{\text{ref}} \vec{E} \cdot \d \vec{l} = \int_y^0 -E_0 \y \cdot \d y \y = E_0 y$$

f) Hvis vi slipper protonet ved et punkt $ y = d/2 $. Hva er det elektriske potensialet i dette punktet. Hvilken vei vil protonet bevege seg --- mot høyere eller lavere elektrisk potensial?

Answer.

Nedover (negativ $ y $-retning) som er mot lavere elektrisk potensial.

Solution.

Det elektriske feltet er $ \vec{E} = - \nabla V $ slik at feltet peker i den retningen som det elektriske potensialet synker. Feltet peker derfor mot lavere potensial. Siden ladningen er positiv, vil kraften på ladningen være $ \vec{F} = q \vec{E} $ som vil ha samme retning som det elektriske feltet. Kraften peker derfor mot lavere elektrisk potensial.

g) Hvis vi tar vekk protonet og i stedet plasserer et elektron i et punkt $ y=d/2 $. Hva er nå det elektriske potensialet i dette punktet? Hvilken vei vil elektronet bevege seg --- mot høyere eller lavere elektrisk potensial?

Answer.

$ V(d/2) = Ed/2 $. Mot høyere elektrisk potensial.

Solution.

Det elektriske potensialet er det samme for positiv og negativ test-ladning, $ V(d/2) = E_0 (d/2) $. Kraften på elektronet vil være $ \vec{F} = - e\vec{E} $ slik at kraften peker motsatt vei av feltet. Siden feltet peker mot lavere elektrisk potensial, vil elektronet bevege seg motsatt vei – mot høyere elektrisk potensial.

h) Synes du spørsmålet Hva er nå det elektriske potensialet var uklart? Hvorfor er det eventuelt uklart? Synes du det gir mening å si det elektriske potensialet til protonet/elektronet eller det elektriske potensialet til det elektriske feltet?