Oppgave
Oppgave: Potensial, felt og krefter
Figuren viser det elektriske potensialet \( V(x) \) langs \( x \)-aksen for en ladningsfordeling. (Vi kjenner ikke detaljene i ladningsfordelingen, men vi har målt eller regnet ut potensialet).
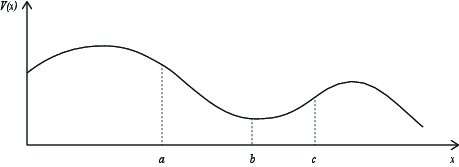
a) Hvilken vei peker det elektriske feltet i punktene \( a,b \) og \( c \)?
\( a \): mot høyre; \( b \): null; \( c \): mot venstre.
Det elektriske feltet er gitt som \( \vec{E} = - \nabla V \) slik at \( E_x = - \d V / \d x \). I punktet \( a \) er stigningstallet negativt, slik at \( E_x \) blir positiv. I \( b \) er stigningstallet tilnærmet lik null, slik at \( E_x \) blir null. I \( c \) er stigningstallet positivt, slik at \( E_x \) blir negativ.
b) Skisser det elektriske feltet \( E_x(x) \).
c) Hvis vi slipper en negativ ladning \( -q \) i punktene \( a \), \( b \) og \( c \), hvilken vei vil ladningen begynne å bevege seg?
\( a \): mot venstre; \( b \): vil ikke bevege seg; \( c \): mot høyre.