Oppgave: Hvor mye strøm går det i en permanent magnet

(AMS 1: Comments on this tutorial from University of Colorado - Boulder:

The focus on this tutorial is to develop an understanding of the concept of bound currents.

This is a particularly strong tutorial. There was a constant hum of discussion, all the students seemed engaged and interested, and misconceptions were resolved. This tutorial had a point, an end goal (to estimate the bound current). In the process of achieving that goal, many relevant topics came up, like magnetic dipoles and bound current. The activity seemed to flow very well.

Part 1 This section took students about 40 minutes to complete. At this point in the semester, students should have developed some ability to question implicit assumptions. In question (i) two students asked how we know that the flat sides of the magnet are the poles (rather than the curved ends), and then checked it with a compass. Questions (i)-(iv) are a simple warmup, and makes the point that the geographic north pole is not the same as the magnetic north pole, which is clarifying for a few students. In question (v), most students drew pictures of little currents canceling out inside the magnet. One group wondered why the field is uniform inside a magnet, and argued that the currents wouldn’t cancel inside the magnet if this were not the case. The instructor pointed out to students that these drawings of currents were of electrons orbiting the nuclei, but that the drawings could also represent electron “spin current” (which is actually the dominant effect). Some groups discussed the direction of the magnetic dipole orientation – the instructor noted that the small dipoles will orient in the same direction as the overall dipole field of the magnet.

Almost every student was confused by the definition of theta in the equation for B of a dipole in question (vi). Some thought this was the angle that the compass needle was deflected, and others thought it was the angle relative to magnetic north. The instructor helped them to resolve this by drawing a current loop (magnetic dipole), sketching its field (which students were familiar with) and identifying theta in order to make the equation match their sketch of the B field. Students had some troubles figuring out what to do with the ruler in order to estimate m (perpendicular to North gives the best estimate). The other difficulty was that students did not realize that the B-field from the magnet would equal the B-field of Earth when everything is aligned as in Figure 2.

One group noticed that the bound current on the outside of the doughnut-shaped magnet flows the opposite direction of the bound current inside the hole. The math of the cross-products for this question should agree with the model and sketch of atomic current in question (iv), and students can be encouraged to make this connection. In the end, each group came to a similar estimate for I (which is similar to our estimate) of 1000-2000 A.)

Vi har lært at strømmer lager magnetiske felt, men hvor mye strøm kreves? Vi har nå alle verktøyene som skal til for å finne ut hvor mye bundet strøm det er en i leketøysmagnet som i Geomag magnet. En Geomag magnet består av to neodym magneter som er forbundet med en jernsylinder med høy permeabilitet. Vi skal bruke enkle hjelpemilder og litt fysikk til å finne ut hvor stor bundet strøm som går i denne magneten for å lage det permanente magnetfeltet.

a) Vi skal i denne oppgaven bruke et kompass. Du kan bruke kompasset som er innebygget i telefonen din eller du kan bruke et fysisk kompass hvis du har tilgang til det. Et fysisk kompass består av en magnetisk nål som geomag magneten du har fått låne. Nordsiden av magneten er markert med nord eller ofte med en pil. Nordsiden svarer til den veien det magnetiske momentet \( \vec{m} = I \vec{S} \) peker som er gitt av strømretningen og høyrehåndsregelen. Figuren viser en kompassnål som ligger på jordens overflate der du er nå. Hvor er den magnetiske nord og sydpolen på jorden?

Answer.

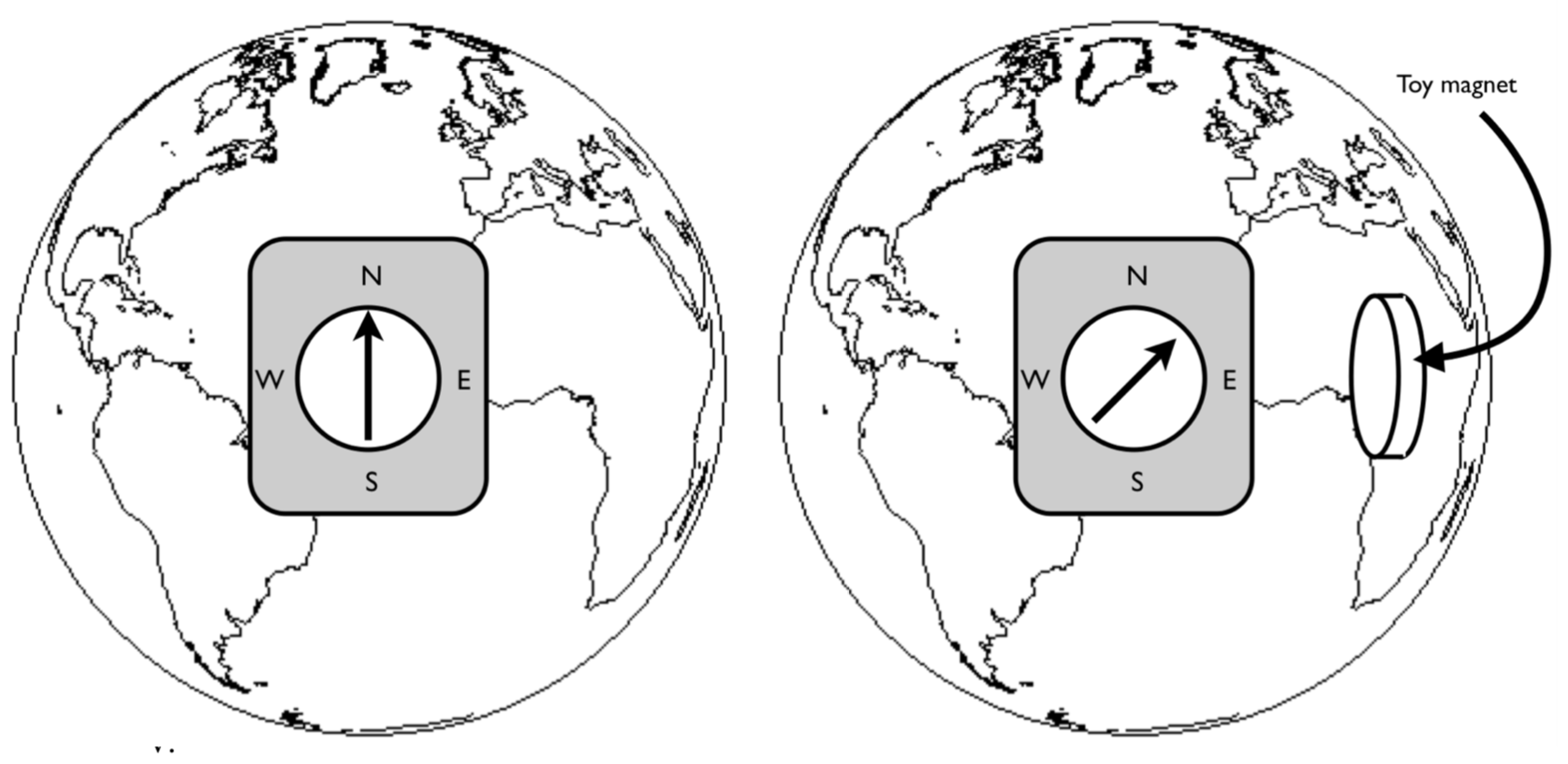
b) I hvilken retning går strømmen inne i jorden?

c) Hold kompasset/telefonen din slik at det peker mot nord. Hvis du holder magneten opp ved siden av kompasset/telefonen, hvilken pol på leketøysmagneten er nærmest kompasset?

d) Hvilken vei går strømmen i magneten?

e) Hva tror du - er det en bundet overflatestrømm, bundet volumstrøm eller begge deler i magneten?

Answer.

f) Ved hjelp av kompasset, magnetetn (og jorda) orietert som i figuren, estimer det magnetiske momentet, \( \vec{m} \). Du trenger å måle avstanden fra magneten til kompasset. Du vil også få bruk for et uttrykk for magnetfeltet fra magneten. For en magnet i origo er magnetfeltet fra magneten i et punkt \( \vec{r} \) tilnærmet gitt som $$ \begin{equation} \vec{B}(\vec{r}) = \frac{\mu_0}{4 \pi} \left[ \frac{3 \rhat (\vec{m} \cdot \rhat) - \vec{m}}{r^3}\right] \, \qquad \, \mu_0 = 4 \pi \times 10^{-7} \text{Tm/A} \tag{1} \end{equation} $$ hvor \( \vec{m} \) er det magnetiske momentet til magneten. Jordas magnetfelt er omtrent \( 5\times 10^{-5} \text{T} \) der hvor vi er.

Diskuter med sidemannen eller gruppen rundt deg hvordan dere kan bruke dette til å bestemme \( \vec{m} \) for magneten. Finn et uttrykk for \( m \) basert på størrelser du kan måle.

Answer.

g) Finn et estimat for den bundne strømmen, \( I_b \).

h) Hva blir det magnetiske feltet inne i permanentmagneten?

i) (Ekstraoppgave) Det er også mulig å måle det magnetiske feltet direkte med telefonen din, f.eks. med programmet Phyphox som er tilgjengelig både på iPhone og Android. Hvordan kan vi bruke en slik måling sammen med teorien over for å finne et estimat for den bundne strømmen \( I_b \)?