Oppgave
Oppgave: Finn fluksen
Finn fluksen \( \Phi_B \) gjennom overflaten \( S \) for disse situasjonene med utgangspunkt i figuren. Orienteringen av overflaten \( S \) er gitt av retningen på kurven eller av en normalvektor på overflaten.
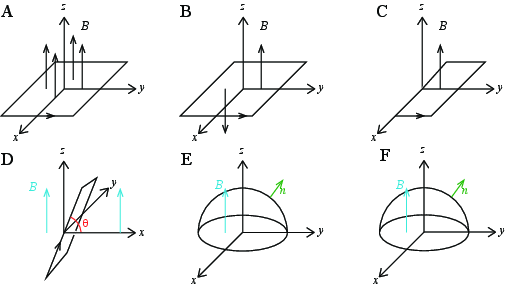
a) (Figur A): En plan, kvadratisk overflate i \( xy \)-planet fra \( -a \) til \( a \) i både \( x \)- og \( y \)-retningen og et homogent magnetfelt \( \vec{B} = B_0 \z \).
\( \Phi_B = 4 a^2 B_0 \).
b) (Figur B): En plan, kvadratisk overflate i \( xy \)-planet fra \( -a \) til \( a \) i både \( x \)- og \( y \)-retninger og et magnetfelt \( \vec{B} = \frac{B_0}{b}x \z \).
\( \Phi_B = 0 \)
c) (Figur C) En plan, rektangulær overflate i \( xy \)-planet fra \( x=0 \) til \( x=a \) og \( y=-a \) til \( y=a \) og et magnetfelt \( \vec{B} = \frac{B_0}{b}x \z \).
d) (Figur D) En plan, kvadratisk overflate med sidekanter \( 2a \) som er rotert en vinkel \( \theta \) om \( y \)-aksen. Et homogent magnetfelt \( \vec{B} = B_0 \z \).
e) (Figur E) En overflate med form som en halvkuleflate med radius \( a \) og et homogent magnetfelt \( \vec{B} = B_0 \z \).
f) (Figur F) En overflate med form som en halvkuleflate med radius \( a \) og et magnetfelt \( \vec{B} = \frac{B_0}{b} r \z \) hvor \( r = \sqrt{x^2 + y^2} \).