Oppgave: Emf på bussen

Faradays lov gjelder uansett hvordan fluksen varierer – om det er kretsen som flytter på seg, om det er feltet som endrer seg med tiden, eller om det er formen på kretsen som endrer seg med tiden. Men hvordan henger dette sammen?

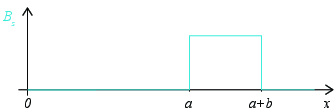
Vi lager en modell som vi skal studere i detalj. Figuren viser en buss som kjører langs \( x \)-aksen med konstant hastighet \( v \). Inne i bussen er det en kvadratisk krets i \( xy \)-planet med sidekant \( d \). Det er et homogent magentisk felt \( \vec{B} = B_0 \z \) mellom \( x=a \) og \( x=a+b \). Du kan anta at \( a>d \).

Ved tiden \( t=0 \) passerer den høyre siden av kretsen \( x=0 \).

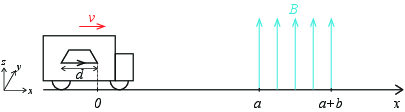
Sett fra veien

Først ser vi på hvordan denne prosessen opptrer for en tilskuer som står på veien.

a) Skisser det magnetiske feltet som funksjon av \( x \).

Answer.

b) Finn posisjonen til høyre side av kretsen som funksjon av tiden, \( x(t) \).

Answer.

c) Finn fluksen gjennom kretsen som funksjon av tiden \( t \).

Answer.

d) Finn den induserte emf'en i kretsen som funksjon av tiden \( t \)

Sett fra bussen

Så ser vi på hvordan denne prosessen opptrer for en tilskuer som står inne i bussen.

e) Skisser det magnetiske feltet i på høyre og venstre side av kretsen som funksjon av tiden.

Answer.

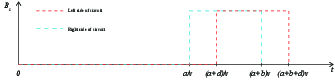
f) Skisser den magnetiske fluksen i kretsen som funksjon av tiden.

Answer.