Oppgave
Oppgave: Finn emf'en
Finn emf'en, både størrelse og retning, som er indusert i krestene i figuren.
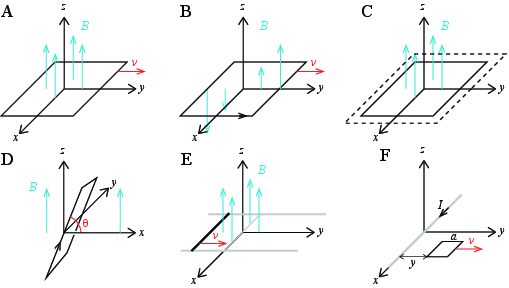
a) (Fig. A) En kvadratisk krets i \( xy \)-planet med sider \( 2a \) beveger seg med konstant hastighet \( \vec{v} \) langs \( x \)-aksen gjennom et homogent magnetisk felt \( \vec{B} = B_0 \z \).
\( e = - \frac{\d \Phi_B}{\d t} = 0 \)
b) (Fig. B) En kvadratisk krets i \( xy \)-planet med sider \( 2a \) beveger seg med konstant hastighet \( \vec{v} \) langs \( x \)-aksen gjennom et magnetisk felt \( \vec{B} = \frac{B_0}{b}y \z \). Venstre side av kretsen er i posisjonen \( y \).
\( e = -\frac{4a^2 v B_0}{b} \)
c) (Fig. C) En kvadratisk krets i \( xy \)-planet utvider seg i alle retninger med hastighet \( v \) i et homogent magnetisk felt \( \vec{B} = B_0 \z \). Ved tiden \( t=0 \) er lengden av sidekanten \( 2a \).
\( e = -B_0(4av + 2v t) \)
d) (Fig. D) En plan, kvadratisk krets med sidekant \( 2a \) roteret en vinkel \( \theta \) rundt \( y \)-aksen. Vinkelen \( \theta \) øker med en vinkelhastighet \( \omega \): \( \theta = \omega t \). Kretsen er i et homogent magnetisk felt \( \vec{B} = B_0 \z \).
\( e = B_0 4 a^2 \omega \sin \theta \)
e) (Fig. E) En krets som består av to lange ledere langs \( y \)-aksen (i grått) og en leder med lengde \( 2a \) som forbinder dem. Den siste siden i kretsen beveger seg langs \( y \)-aksen med hastighet \( \vec{v} \) og passerer \( x \)-aksen ved \( t=0 \). Det er et homogent magnetisk felt \( \vec{B} = B_0 \z \).
\( e = - B_0 v 2a \quad (t>0) \qquad B_0 v 2a \quad (t < 0) \)
f) (Fig. F) Det går en strøm \( I \) langs en ledning langs \( x \)-aksen. En kvadratisk krets med side \( a \) ligger i \( xy \)-planet i en avstand \( y \) fra \( x \)-aksen. Kretsen beveger seg i positiv \( y \)-retning med hastigheten \( \vec{v} \).
\( e = \frac{I\mu_0 a}{2 \pi} \left( \frac{1}{y+a} - \frac{1}{y}\right) v \)