Oppgave
Oppgave: Felt og \( \vec{R} \)-vektor for en enkelt ladning
En ladning \( -Q \) er plassert i origo.
a) Tegn inn \( \vec{R} \)-vektoren som du vil bruke til å finne det elektriske feltet fra ladningen i punktet \( (a,0) \).
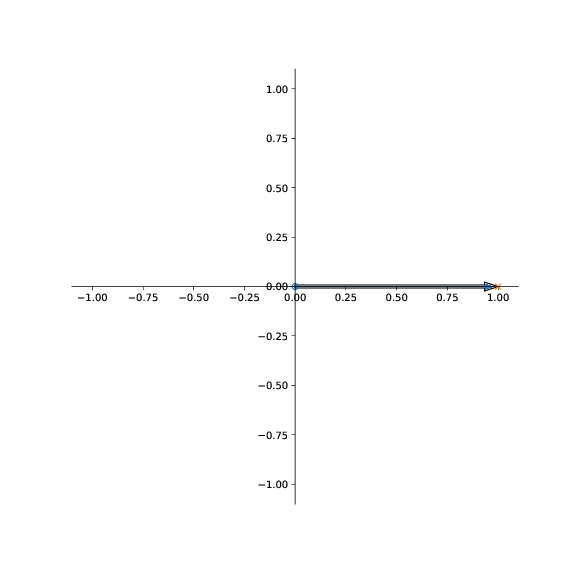
b) Tegn inn \( \vec{R} \)-vektoren som du vil bruke til å finne det elektriske feltet fra ladningen i punktet \( (0,a) \).
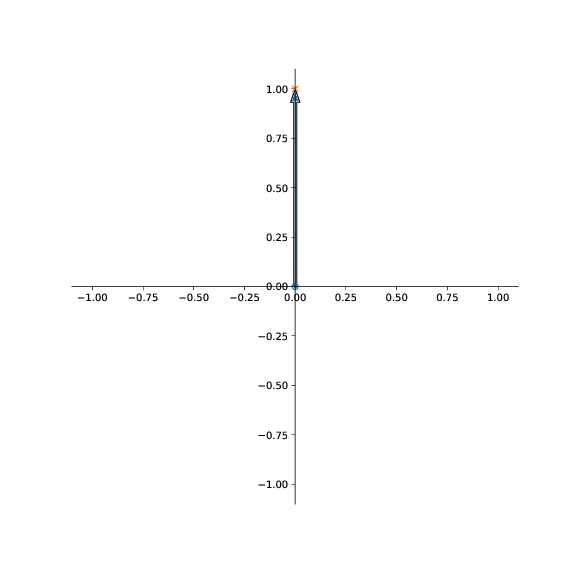
c) Finn det elektriske feltet i punktet \( (a,a) \).
Vi finner det elektriske feltet ved først å finne \( \vec{R} = \vec{r} - vec{r}_1 \) hvor \( \vec{r} = (a,a) \) og \( \vec{r}_1 \) er posisjonen til ladningen som er \( \vec{r}_1 = (0,0) \), slik at $$\vec{R} = (a,a) - (0,0) = (a,a)$$
Dermed er det elektriske feltet i punktet \( \vec{r} = (a,a) \) gitt som $$\vec{E}(\vec{r}) = \frac{-Q}{4 \pi \epsilon_0}\frac{\vec{R}}{R^3} = \frac{-Q}{4 \pi \epsilon_0}\frac{(a,a)}{(2a^2)^{3/2}} = \frac{Q}{4 \pi \epsilon_0 a^2 2^{3/2}}(-1,-1)$$