$$ \renewcommand{\vec}[1]{\mathbf{#1}} \newcommand{\x}{\mathbf{\hat{x}}} \newcommand{\y}{\mathbf{\hat{y}}} \newcommand{\Rhat}{\mathbf{\hat{R}}} \renewcommand{\d}{\mathrm{d}} $$

Oppgave

Oppgave: Tre ukjente ladninger

Tre ladninger $ q_1 $, $ q_2 $ og $ q_3 $ ligger langs $ x $-aksen i punktene $ (-a,0) $, $ (0,0) $ og $ (a,0) $ respektivt. Alle ladningene har samme størrelse ($ |q_1| = |q_2| = |q_3| $). Figuren viser det elektriske feltet $ E_x(x) $ langs $ x $-aksen. Hvilke fortegn har de tre ladningene?

Answer.

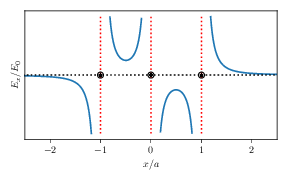
$ q_1>0 $, $ q_2 < 0 $, $ q_3>0 $

Solution.

$ q_1>0 $, $ q_2 < 0 $, $ q_3>0 $

Kontinuerlig ladningsfordeling