Oppgave
Oppgave: Ladning fra en ladningstetthet
En romladningstetthet \( \rho \) er gitt som: $$ \begin{equation} \rho(\vec{r}) = \left\{ \begin{array}{cc} C & \text{ for } r < a \\ 0 & \text{ for } r \ge a \end{array}\right. \tag{5} \end{equation} $$
a) Lag en skisse av ladningstettheten. (Vi lager alltid skisser av systemet i fysikk).
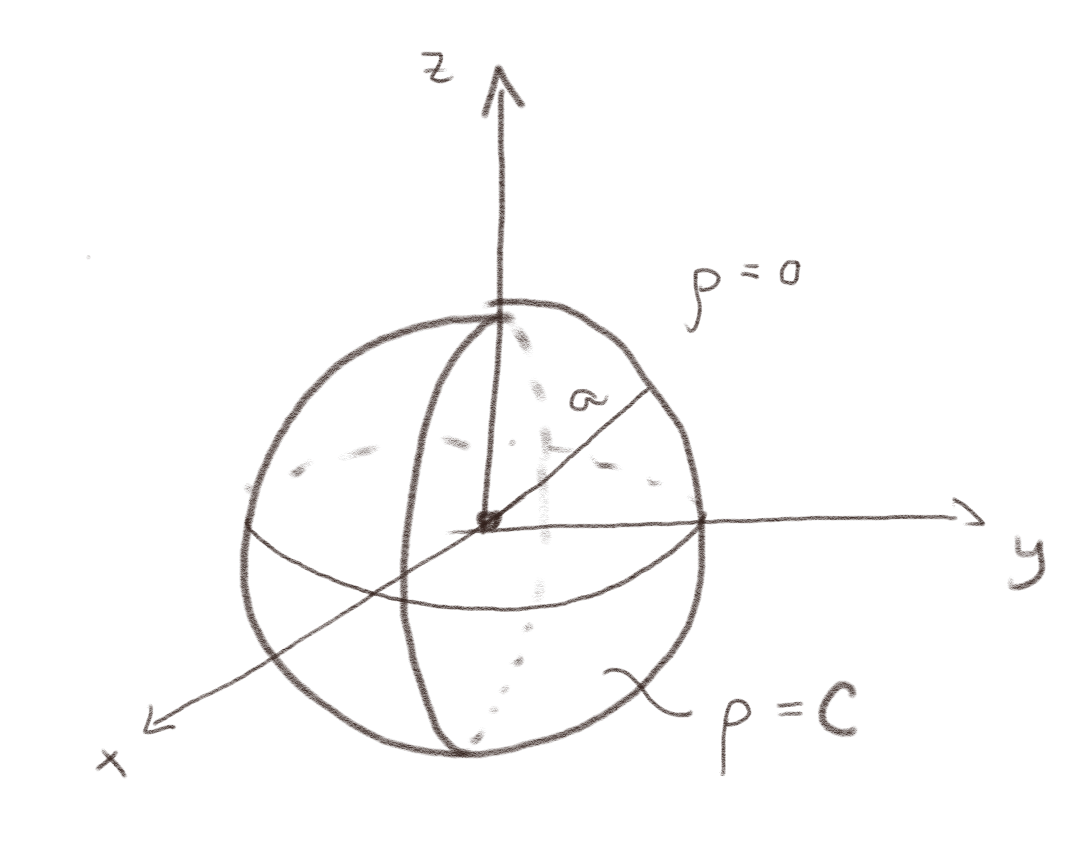
b) Hvor mye ladning, \( Q(r) \), er innenfor en radius \( r \) fra origo?
Hvis \( r \) er mindre eller lik \( a \) så må vi finne ut hvor mye av ladningen som er innenfor en radius \( r \). Det er gitt som volumet ganger med romladningstettheten: $$ \begin{equation*} Q(b) = \int \rho \d v = \int_0^r 4 \pi r^2 \rho \d r = \frac{4\pi}{3} r^3 \rho = \frac{4\pi}{3}r^3 C \end{equation*} $$ Mens når \( r \) er større enn \( a \), så vil det kun være kulen med ladning innenfor \( a \) som innholder ladning, mens område utenfor ikke inneholder noe ladning. Da er volumet gitt som volumet av en kule med radius \( a \) og ladningen er $$Q = \frac{4\pi}{3}a^3 C$$
Slik at ladningen som funksjon av \( r \) blir: $$ \begin{equation*} Q(r) = \left\{ \begin{array}{cc} \frac{4\pi}{3}r^3 C & \text{ for } r < a \\ \frac{4\pi}{3}a^3 C & \text{ for } r \ge a \end{array}\right. \end{equation*} $$