Seminar uke 01: Elektrisk felt

Oppgave

Oppgave: Lang ledning

En tynn, lang ledning ligger langs $ x $-aksen og skjærer $ y $-aksen i en avstand $ a $ fra $ x $-aksen. En lengde $ L $ av ledningen har en ladning $ Q $. (Du kan anta at ledningen er uendelig lang og at den har en uniformt fordelt ladning).

a) Lag en tegning av systemet.

Answer.

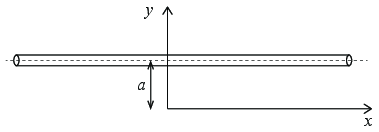
Vi skal finne det elektriske feltet i et punkt $ \vec{r} = (x,0,0) $ langs $ x $-aksen.

b) Uten å regne ut noe, hvilken vei tror du det elektriske feltet vil peke i punktet $ (x,0,0) $?

Answer.

Normalt på ledningen og vekk fra ledningen, dvs. i negativ $ y $-retning.

Solution.

Det vil peke normalt vekk fra ledningen. Hvorfor normalt på ledningen? Det følger av et symmetri-argument. Anta at det elektriske feltet har en komponent langsmed ledningen. Hvis vi roterer ledningen en vinkel $ \pi $ (om $ y $-aksen) så vil ledningen være akkurat identisk som før rotasjonen. Da må også det elektriske feltet måtte være identisk. Men hvis feltet har en komponent som ikke er normal på ledningen, så vil denne komponenten også ha rotert en vinkel $ \pi $ (om $ y $-aksen). Da vil ikke feltet være identisk, med mindre denne komponenten er null. Altså må komponenten være null.

c) Den venn Pia sier at hvis du ønsker å finne det elektriske feltet i en posisjon $ (x,0,0) $ så kan du like gjerne regne ut det elektriske feltet i punktet $ (0,0,0) $ fordi det blir det samme resultatet. Har Pia rett? Begrunn hvorfor eller hvorfor ikke Pia har rett.

Answer.

Hun har rett.

d) Tegn inn et lite linjelement $ \d l $ av ledningen i posisjonen $ (x',a,0) $. Hva er ladningen til dette linjeelementet?

Answer.

$ \d q = (Q/L) \d l $

Solution.

Ladningstettheten er gitt som $ \rho_l = Q/L $ slik at et linjestykke med lengde $ \d l $ har ladningen $ \d q = \rho_l \d l = (Q/L) \d l $.

e) Hva er $ \vec{R} $-vektoren du må bruke for å finne bidraget fra linjeelementet $ \d l $ til det elektriske feltet i punktet $ (0,0,0) $?

Answer.

$ \vec{R} = (-x',-a,0) $

Solution.

Vi finner $ \vec{R} $-vektoren som $ \vec{R} = \vec{r} - \vec{r}' $ hvor $ \vec{r} = (0,0,0) $ og $ \vec{r}' = (x',a,0) $ slik at $ \vec{R} = (-x',-a,0) $.

f) Hva er bidraget $ \d \vec{E} $ til $ \vec{E} $-feltet fra dette linjeelementet?

Answer.

$$\d \vec{E} = \frac{(Q/L)\d x'}{4 \pi \epsilon_0} \frac{(-x',-a,0)}{((x')^2 + a^2)^{3/2}} $$

Solution.

Bidraget er gitt av Coloumbs lov og blir $$ \begin{equation*} \d \vec{E} = \frac{\d q}{4 \pi \epsilon_0} \frac{\vec{R}}{R^3} = \frac{(Q/L)\d x'}{4 \pi \epsilon_0} \frac{(-x',-a,0)}{((x')^2 + a^2)^{3/2}} \end{equation*} $$

g) Skriv opp integralet for å finne $ \vec{E} $-feltet --- skriv det helt ut på koordinat-form eller skriv et integral for $ x $- og et for $ y $-komponenten.

Hint.

Du skal kun skrive opp integralet. Du skal ikke regne det ut.

Answer.

$$E_x = \int_{-\infty}^{\infty} \frac{(Q/L)\d x'}{4 \pi \epsilon_0} \frac{-x' \x }{((x')^2 + a^2)^{3/2}}$$ $$ E_y = \int_{-\infty}^{\infty} \frac{(Q/L)\d x'}{4 \pi \epsilon_0} \frac{-a \y }{((x')^2 + a^2)^{3/2}} $$

Solution.

Vi finner integralet som $$ \begin{equation*} \vec{E} = \int_{-\infty}^{\infty} \frac{(Q/L)\d x'}{4 \pi \epsilon_0} \frac{(-x',-a,0)}{((x')^2 + a^2)^{3/2}} \end{equation*} $$ Vi kan dele dette opp i to integraler i $ x $- og $ y $-retningen. $$ \begin{equation*} E_x = \int_{-\infty}^{\infty} \frac{(Q/L)\d x'}{4 \pi \epsilon_0} \frac{-x' \x }{((x')^2 + a^2)^{3/2}} \end{equation*} $$ $$ \begin{equation*} E_y = \int_{-\infty}^{\infty} \frac{(Q/L)\d x'}{4 \pi \epsilon_0} \frac{-a \y }{((x')^2 + a^2)^{3/2}} \end{equation*} $$