Oppgave
Oppgave: Strømtetthet
Det går en strøm \( I \) gjennom en leder med sidekanter \( a \) og lengde \( L \). Anta at strømtettheten er uniform inne i lederen.
a) Hva er strømtettheten i lederen?
\( \vec{J} = I/a^2 \x \)
Strømtettheten er \( \vec{J} = I/A \x = I/a^2 \x \).
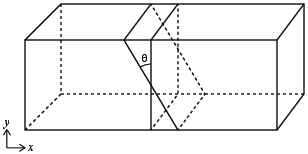
b) Vi lager en overflate \( S \) som danner en vinkel \( \theta \) med en overflate som er normal på sylinderaksen som vist i figuren. Vis at strømmen er den samme for alle vinkler \( -\pi/2 < \theta < \pi/2 \).
Det kan være lurt å bruke vinkelen mellom normalvektorene.
Husk at overflaten \( S \) også avhenger av vinkelen \( \theta \).
Strømmen er gitt som \( I = \int_S \vec{J} \cdot \d \vec{S} = \vec{J} \cdot S \nhat \) hvor \( \nhat \) er normalvektoren til overflaten. Normalvektoren har retningen \( \nhat = (\cos \theta, \sin \theta) \). Hva er arealet til overflaten \( S \)? \( A = a \, a/\cos \theta \). Dermed blir $$I = \vec{J} \cdot S \nhat = \frac{I}{a^2} \frac{a^2}{\cos \theta} \, \cos \theta = I$$ som den skulle være.
c) Hva blir strømmen \( I \) hvis \( \theta > \pi/2 \)?
Negativ.