Seminar uke 06: Strøm og motstand

Oppgave

Oppgave: Motstandsgymnastikk

En motstand som har et tverrsnittsareal $ A = a \times a $, en lengde $ L $ og er laget av et materiale med ledningsevne $ \sigma $ har motstanden $ R = L/(\sigma a^2) $.

a) Vi deler motstanden i to på midten slik at vi få to like lange deler med lengde $ L/2 $ som er koblet sammen på midten. Hva blir motstanden til det systemet av to motstander?

Answer.

$ R = L/(\sigma a^2) $.

Solution.

Hver motstand har motstanden $ R = (L/2)/(\sigma a^2) $. De er koblet i serie med hverandre slik at den samlede motstanden blir $ R_T = R+R = L/(\sigma a^2) $.

b) Vi deler motstanden i små biter av lengden $ \d x $. Vis hvordan du kan finne det totale motstanden til en motstand av lengde $ L $ ved et integral.

Answer.

$ R = \int_0^L \d x / (\sigma a^2) $

Solution.

Hver lille bit med lengde $ \d x $ har en motstand $ \d R = \d x/(\sigma a^2) $. Alle bitene er koblet i serie med hverandre. Den totale motstanden blir da $ R = \int_0^L \d x / (\sigma a^2) = L /(\sigma a^2) $.

Denne metoden med å dele inn systemet i små deler som så kan summere opp motstanden til gjennom et integral kan anvendes flere steder. Anta at vi ser på en motstand som består av en sektor $ \theta $ av en sylinder med indre radius $ a $ og ytre radius $ b $ og høyde $ h $ hvor strømmen går fra den indre radiusen til den ytre radiusen.

c) Hva blir motstaden $ \d R $ til en tynn skive fra $ r $ til $ r + \d r $?

Answer.

$ \d R = \d r/(\sigma r \theta h) $.

Solution.

Motstanden blir $ \d R = \d r /(\sigma A) $ hvor $ A = r \theta h $ slik at $ \d R = \d r/(\sigma r \theta h) $.

d) Hva blir motstanden $ R $ til hele systemet?

Answer.

$ R = \frac{1}{\sigma h \theta} \ln \frac{b}{a} $

Solution.

Vi finner motstanden ved å integrere fra $ a $ til $ b $: $$ \begin{equation*} R = \int_a^b \frac{\d r}{\sigma h \theta r} = \frac{1}{\sigma h \theta} \ln \frac{b}{a} \; . \end{equation*} $$

Men denne metoden virker ikke alltid. Figuren under viser en motstand med tverrsnitt $ a \times a $ og lengde $ L $ som er kappet i mange små biter med lengde $ \d x $, men hvor hver bit er forskøvet litt langs $ y $-aksen, slik at motstanden strekker seg fra $ y=0 $ til $ y=h $ og danner en vinkel $ \theta $ med $ x $-aksen.

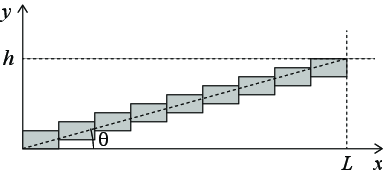
e) Hvorfor kan man ikke bruke samme metode her og summere opp alle bidragene og finne at motstanden er $ R = L/(\sigma a^2) $?

f) Kan du finne et uttrykk for motstanden til dette systemet ved å anta at volumet er konstant når materialet har blitt strukket slik at motstanden strekker seg fra $ x=0 $ til $ x=L $ og $ y=0 $ til $ y=h $?

Answer.

$ R = L/(\sigma a^2 \cos^2 \theta) $.

Solution.

Lengden er i så fall $ L/\cos \theta $. Men hva er tverrsnittarealet? For at volumet skal være konstant så må en av lengden $ a $ endre seg til $ a' $. Hva blir denne? Det kan vi se geometrisk direkte at den blir $ a \cos \theta $. Alternativt ser vi at $ V = L a^2 = L/\cos \theta a a' $ og dermed at $ a' = a \cos \theta $. Da blir motstanden $ R = L/(\sigma a^2 \cos^2 \theta) $. Den går derfor mot uendelig når $ \theta $ går mot $ \pi/2 $.

Merk at dette er grunnen til at vi ikke kan finne motstanden til en konisk motstand ved å kutte den i små sylindere og så summere bidragene fra alle sylindrene.