Oppgave
Oppgave: Magnetisk felt fra et strøm-element
Figuren viser et strøm-element \( I \d \vec{l} = I \d l \y \) som er plassert i origo. Hvilken retning har det magnetiske feltet i punktene? (Vær bevisst på hva som er \( \vec{R} \)-vektor i hvert enkelt tilfelle).
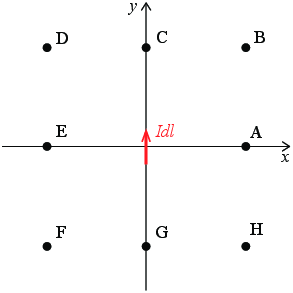
a) Punkt A?
\( -\z \)
b) Punkt B?
\( -\z \)
c) Punkt C?
\( \vec{0} \)
d) Punkt D?
\( +\z \)
e) Punkt E?
\( \z \)
f) Punkt F?
\( \z \)
g) Punkt G?
\( \vec{0} \)
h) Punkt H?
\( -\z \)
Vi gjør tilsvarende oppgave for et strøm-element \( I \d \vec{l} = I \d l \z \) som kommer opp gjennom \( xy \)-planet i figuren. Hvilken retning har det magnetiske feltet i punktene?
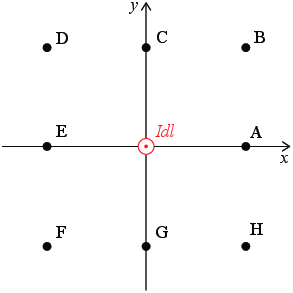
i) Punkt A?
j) Punkt B?
k) Punkt C?
l) Punkt D?
m) Punkt E?
n) Punkt F?
o) Punkt G?
p) Punkt H?
Nå har du blitt en ekspert. La oss endre litt på spørsmålet. Hva om vi plasserer et strømelement \( I \d \vec{l} = -I \d l \z \) og i stedet finner størrelsen og retningen på det magnetiske feltet i origo? Figuren viser strømelementet plassert i posisjonene A-H, men du skal kun se på ett enkelt strøm-element av gangen. Først elementet plassert i posisjon A, så et element plassert i punkt B og så videre.
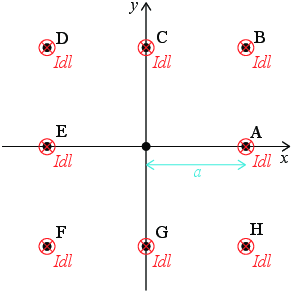
q) Punkt A?
r) Punkt B?
s) Punkt C?
t) Punkt D?
u) Punkt E?
v) Punkt F?
w) Punkt G?
x) Punkt H?