Seminar uke 08: Magnetisk felt

Oppgave

Oppgave: Sammenlikning av linjeladning og linjestrøm

Figuren viser to systemer. Systemet til venstre viser en linjeladning og systemet til høyre viser en linjestrøm. Vi skal sammenlikne de to systemene for å se hvordan vi kan overføre ferdighetene vi har i å analysere og regne på linjeladninger til å kunne regne på linjestrømmer. Det er viktige likhetspunkter og forskjeller som vi skal se på i detalj.

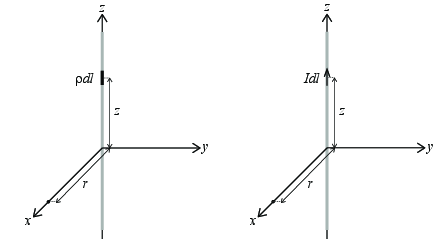
Vi starter med å repetere hvordan vi fant feltet for linjeladningen i systemet til venste. Vi skal finne bidraget til det elektriske feltet i punktet $ (r,0,0) $ fra ladningselementet $ \rho \d l $ i punktet $ (0,0,z) $.

a) Tegn inn $ \vec{R} $-vektor i figuren og finn et uttrykk for $ \vec{R} $-vektor.

Answer.

$$\vec{R} = (r,0,-z)$$

b) Hvordan kunne du argumentere for at det elektriske feltet kun vil ha en radiell komponent – dvs. at det kun vil være en komponent i $ x $-retningen i et punkt langs $ x $-aksen.

Answer.

For hvert ladningselement $ \rho \d l $ vil det også finnes et ladningselement symmetrisk om $ xy $-planet, og $ z $-bidraget fra hver av disse komponentene vil kansellere.

c) Skriv ned bidraget $ \d E_x $ til det elektriske feltet i punktet $ (r,0,0) $.

Answer.

$$\d E_x = \frac{\rho \d l}{4 \pi \epsilon_0} \frac{R_x}{R^3} = \frac{\rho \d l}{4 \pi \epsilon_0} \frac{r}{(z^2 + r^2)^{3/2}} \; . $$

d) Skriv ned integralet du må løse for å finne det totale elektriske feltet. Hva blir integralet? (Det er helt greit å skrive svaret rett ned, hvis du husker det eller du er rask med Gauss lov).

Answer.

$$E_x = \int_{- \infty}^{\infty} \frac{\rho}{4 \pi \epsilon_0} \frac{r}{(z^2 + r^2)^{3/2}} \, \d z = \frac{\rho}{2 \pi \epsilon_0 r}$$

Da er vi klar for å se på et liknende problem – en linjestrøm – som er vist i systemet til høyre. Vi skal finne bidraget til det magnetiske feltet i punktet $ (r,0,0) $ fra strømelementet $ I \d \vec{l} = I \d l \z $ i punktet $ (0,0,z) $.

e) Tegn inn $ \vec{R} $-vektor i figuren og finn et uttrykk for $ \vec{R} $-vektor.

Answer.

$$\vec{R} = (r,0,-z)$$

f) Hvilken retning vil bidraget til $ \vec{B} $-feltet ha for alle strømelementene langs $ z $-aksen?

Answer.

Vi ser av høyrehåndsregelen at alle bidragene blir rettet langs $ y $-aksen.

g) Finn bidraget $ \d \vec{B} $ til det magnetiske feltet i punktet $ (r,0,0) $.

Answer.

$$\d \vec{B} = \frac{\mu_0}{4 \pi}\frac{I \d l r \y}{(r^2 + z^2)^{3/2}}$$

h) Skriv ned integralet du må løse for å finne det totale magnetiske feltet.

Answer.

$$\vec{B} = \int_{-\infty}^{\infty} \frac{I \mu_0}{4 \pi} \frac{r \y}{(z^2 + r^2)^{3/2}} \, \d z$$

i) Kan du skrive ned løsningen på integralet direkte ved å sammenlikne med resultatet du fikk for det elektriske feltet?

Answer.

$$\vec{B} = \frac{I \mu_0}{2 \pi r} \y$$

j) Kan du kort oppsummere forskjellene mellom de to fremgangsmåtene?

Answer.

Den viktigste forskjellen er forskjellen mellom å bruke $ \vec{R} $ direkte for å finne det elektriske feltet og $ \d \vec{l} \times \vec{R} $ for å finne det magnetiske feltet.