Oppgave
Oppgave: Strømsløyfe i magnetfelt
En liten kvadratisk strømsløyfe med sidekant \( a \) plasseres i \( xy \)-planet i et magnetfelt \( \vec{B} = B_0 \y \) som vist i figuren.
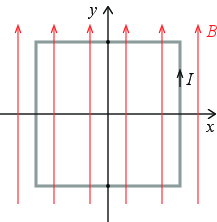
a) Hva er netto kraft på strømsløyfen?
$$0$$
b) Hva er kraftmomentet om \( x \)-aksen?
$$\vec{\tau} = - I a^2 B_0 \x$$
c) Forklar hvordan man kan bruke en strømsløyfe som dette til å måle retningen på et magnetisk felt.
Strømelementet vil rettet seg inn slik at normalvektoren til strømelementet vil peke i retning av det magnetiske feltet.