Oppgave
Oppgave: Ned fra fjellet
Skalarfeltet \( h(x,y) \), som er skissert i figuren, varierer kun langs \( x \)-aksen.
Figure 3
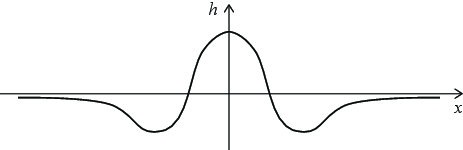
a) Skisser gradienten, \( \nabla h \), i \( xy \)-planet.
b) Hvor er har gradienten størst og minst magnitude?
c) Hvis jeg vil finne laveste punkt, hvordan kan jeg bruke gradienten til å finne det?
d) Kan gradienten være null i et punkt uten at overflaten (lokalt sett) er et plan?
Solution.
Nei. Hvis gradienten er null, så er den deriverte i både \( x \) og \( y \)-retningen null. Da vil også den deriverte i andre retninger være null. Dermed må overflaten være lokalt flat.