Oppgave
Oppgave: Ledere og elektriske felt
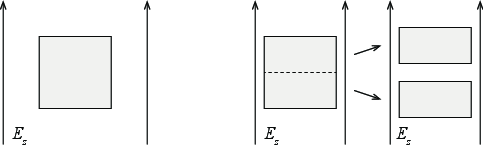
En terning laget av en (ideell) leder plasseres inn i et elektrisk felt \( \vec{E} = E_z \) som vist i figuren til venstre.
a) Hva blir det elektriske feltet inne i terningen?
0
Det elektriske feltet inne i en leder er alltid null.
b) Skisser ladningsfordelingen på terningen.
Positive ladninger øverste flate og negative ladninger på nederste flate. Ingen ladninger inne i terningen.
Ladningsfordelingen må lage et elektrisk felt som virker i motsatt retning av det ytre feltet, slik at det totale feltet blir null.
c) Er det elektriske feltet rundt terningen homogent?
Nei
Dette svaret krever litt omstendelighet. Hvis terningen hadde vært et uendelig bredt plan, så hadde det vært en uniform tetthet av ladning på overflaten. Det hadde laget et uniformt felt inne i planet som hadde motvirket det ytre homogene feltet.
Men terningen er ikke uendelig lang. Derfor kan ikke ladningsfordelingen være homogen nær kanten av terningen. Og dermed vil heller ikke feltet være homogent nær kanten.
Akkurat hvordan feltet blir kan være vanskelig å se. Jeg har gjort en hurtig beregning med Laplace likning for å illustrere dette.

Mens terningen er inne i det elektriske feltet, kapper din venn Q lynraskt terningen i to biter som vist i figuren til høyre. Du har nå to like store, halve terninger inne i det homogene elektriske feltet.
d) Hva blir nå det elektriske feltet inne i den øverste halve terningen?
0
e) Hva blir ladningsfordelingen i de to terningene?
Sjekk at feltet blir null der det skal være null med den fordelingen du har valgt!
\( +Q \) på den øverste overflaten.
Hmmm. Denne oppgaven er litt vanskelig ved første øyekast. Først innsert vi at den øverste halve terningen har ladningen \( +Q \) mens den nederste har ladningen \( -Q \).
Poenget er at ladningene plasseres på et slikt vis at feltene inne i lederne blir null. Hvordan kan vi få det til? Det er overraskende enkelt. Vi plasserer ladningen \( +Q \) på den øverste flaten til en øverste halve terningen og ladnigen \( -Q \) på den nederste flaten til den nederste halve terningen. Da blir feltene inne i de to lederne null. (Og feltet mellom de to lederne blir også null).
Vi har da laget et slags en-dimensjonalt Faraday bur!
f) Hva blir det elektriske feltet i området mellom de to terningbitene?
0