Oppgave
Oppgave: Sandwich
Vi bygger en lur kondensator som består av tre parallelle ledende plater med tykkelse \( d \), avstand \( h \), og areal \( L \). Du kan anta at arealet \( L \) er så stort at du kan se bort fra kanteffekter. (Se figuren).

a) Hva er det elektriske feltet fra et uendelig plan i \( xy \)-retningen med overflateladningstetthet \( \rho_S = Q/A \)? (Her holder det at du husker det eller slår opp resultatet. Vi trenger det snart).
\( E_z = \rho_S/(2 \epsilon_0) \) for \( z>0 \) og \( E_z = - \rho_S/(2 \epsilon_0) \) for \( z < 0 \).
Anta at den midterste lederen har ladning \( -Q \) og at hver av de to andre lederne har ladningen \( Q/2 \).
b) Hvordan blir ladningsfordelingen på lederne?
Tenk nøye gjennom hvordan ladningene må plasseres og hvilke prinsipper du brukere for å komme fram til det.
Husk at du må summere feltene fra alle ladningene!

c) Hva blir det elektriske feltet normalt på lederne, \( E_z(z) \)? Du kan bruke resultatet du skrev ned i oppgave a)
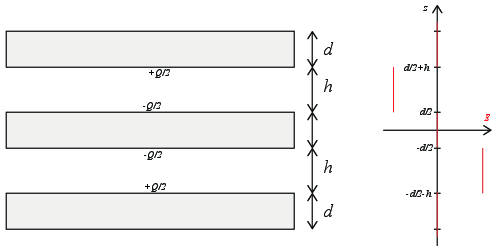
Det elektriske feltet i området \( d/2 < z < d/2+h \) er feltet fra to plan med ladninger \( Q/2 \) og \( -Q/2 \). Det elektriske feltet blir derfor \( E_z = 2(Q/2/A)/(2 \epsilon_0) = Q/(2 A \epsilon_0) \).
d) Hva blir potensialforskjellen mellom positiv og negativ leder?
\( \frac{Qh}{2 A \epsilon_0} \)
Avstanden er \( h \) fra \( -Q/2 \) til \( Q/2 \). Det elektriske feltet i dette området er \( Q/(2A\epsilon_0) \) slik at potensialforskjellen er $$V = \int_{d/2}^{d/2+h} E_z \d z = \frac{Qh}{2 A \epsilon_0}$$
e) Hva blir kapasitansen til systemet?
\( C = \frac{2 A \epsilon_0}{h} \)
f) Hvordan tolker du dette resultatet?
Dette kan vi tolke som at kondensatoren har et effektivt areal på \( 2A \).
(Hvis du vil se fortsettelsen på denne oppgaven kan du se på Eksamen H2020 Oppgave 1. Merk at oppgavesettet for 2020 ble noe i vanskeligste laget for dette emnet, selv om det er en vakker oppgave)