Oppgave
Oppgave: Laplace operatoren i en dimensjon
Vi kaller \( \nabla^2 \) for Laplace operatoren. La oss se litt hvilke egenskaper den har. Figuren under viser to forskjellige potensielle potensialer \( V(x) \).
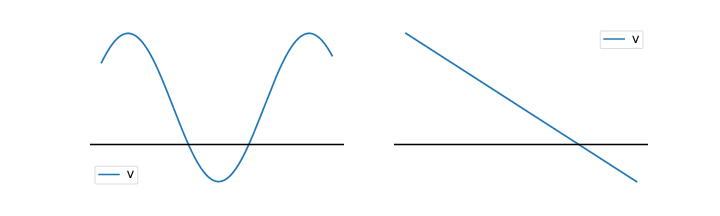
a) Hvor er Laplace-operatoren anvendt på funksjonen \( V(x) \), \( d^2 V/dx^2 \), negativ, null eller positiv i de to figurene?
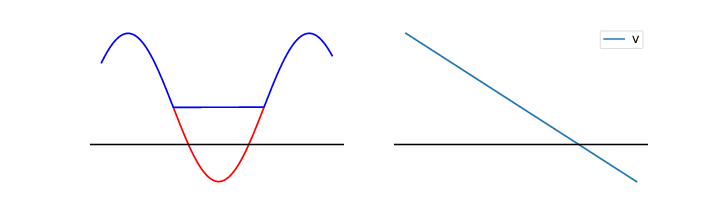
Rød: positiv, Blå: negativ
b) Kan potensialet, \( V(x) \), til venstre i figuren være en løsningen av Laplace likning?
Nei
Figuren til venstre kan ikke være en løsning av Laplace likning fordi \( \nabla^2 V \) kun er null i noen enkeltpunkter.
c) Kan potensialet, \( V(x) \), til venstre i figuren være en løsning av Poissons likning --- og hvordan ser i så fall ladningsfordelingen ut?
Ja, med en ladningsfordeling som har samme form som funksjonen som er skissert.
Figuren til venstre kan være en løsning av Poissons likning. Hvis vi antar at \( V(x) \) er tilnærmet en sinus (hvilken den er), så er den andrederiverte gitt som minus funksjonen. Ladningsfordelingen er derfor omtrent gitt som minus funksjonen som er skissert.
d) Kan potensialet, \( V(x) \), til høyre i figuren være en løsningen av Laplace likning?
Ja
Figuren til høyre er en løsning av Laplace likning fordi \( \nabla^2 V \) er null overalt.
e) Kan potensialet, \( V(x) \), til høyre i figuren være en løsningen av Poissons likning?
Ja
Figuren til høyre er en løsning av Laplace likning fordi \( \nabla^2 V \) er null overalt. Den er derfor også en løsning av Poissons likning, men med en ladningsfordeling som er uniformt null.