Oppgave
Oppgave: Fortegnet til den diskrete Laplace operatoren
Den diskrete Laplace operatoren er altså: $$\bar{\nabla^2} V = \frac{1}{\Delta x^2}\left( V(x+ \Delta x) + V(x - \Delta x) - 2V(x) \right) $$
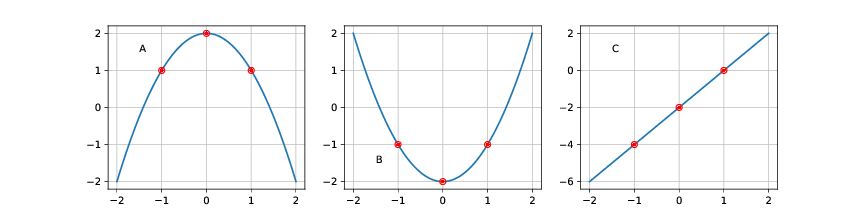
Figuren viser tre forskjellige funksjoner \( V(x) \).
a) Hva blir den diskrete Laplace-operatoren i \( x=0 \) i tilfelle A?
\( -2 \)
$$V(0) \simeq (V(-1)+V(1)-2V(0))/1 = (1+1-2 \cdot 2)/1 = -2$$
b) Hva blir den diskrete Laplce-operatoren i \( x=0 \) i tilfelle B?
\( +2 \)
$$V(0) \simeq (V(-1)+V(1)+2V(0))/1 = (-1+-1+2 \cdot 2)/1 = +2$$
c) Hva blir den diskrete Laplce-operatoren i \( x=0 \) i tilfelle C?
\( 0 \)
$$V(0) \simeq (V(-1)+V(1)-2V(0))/1 = (-4+0-(2*-2))/1 = 0$$