Oppgave
Oppgave: Laplace-operatoren i to og tre dimensjoner
Figuren viser eksempler på potensialflater \( V(x,y) \).
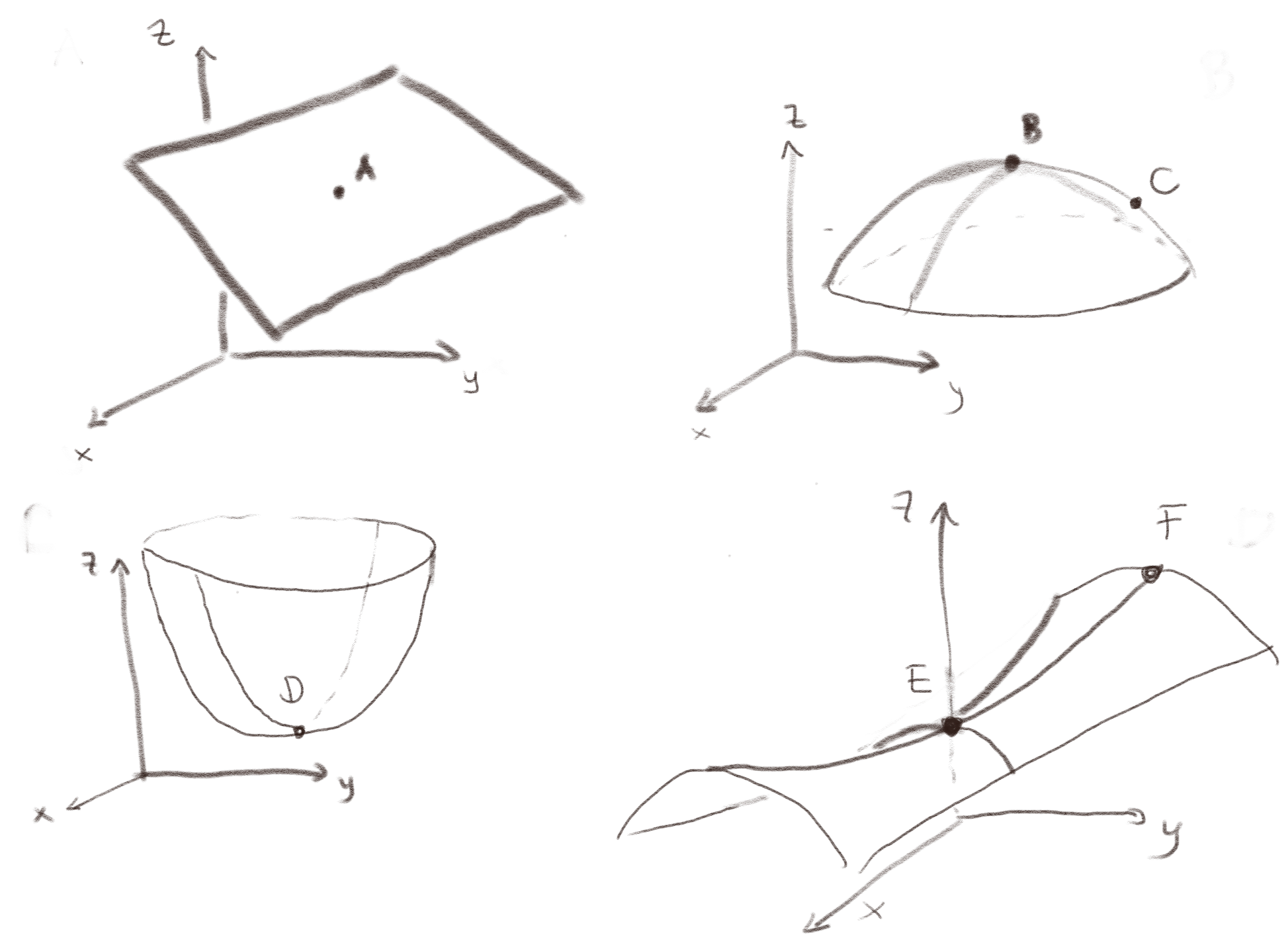
a) Hva er fortegnet til Laplace-operatoren anvendt på \( V(x,y) \) i punktet A?
0
b) Hva er fortegnet til Laplace-operatoren anvendt på \( V(x,y) \) i punktet B?
Negativt
c) Hva er fortegnet til Laplace-operatoren anvendt på \( V(x,y) \) i punktet C?
Negativt
d) Hva er fortegnet til Laplace-operatoren anvendt på \( V(x,y) \) i punktet D?
Positivt
e) Hva er fortegnet til Laplace-operatoren anvendt på \( V(x,y) \) i punktet E?
Mulig med positivt, negativt eller null, men tegningen tyder på negativt.
Her må vi sammenlikne de to krumningene. Det ser ut som om den positive krumningsradiusen i \( x \)-retningen er større enn den negative i \( y \)-retningen, slik at den andrederiverte i \( x \)-retningen blir mindre enn den andrederiverte i \( y \)-retningen. Dermed vil den negative retningen dominere.
f) Hva er fortegnet til Laplace-operatoren anvendt på \( V(x,y) \) i punktet F?
Mulig med positivt, negativt eller null, men tegningen tyder på negativt.
Samme svar som for E.
g) Hvilke av disse flatene kan være en løsning av Laplace likning?
A og kanskje E/F.
Laplace-operatoren i to dimensjoner er $$\nabla^2 V = \frac{\partial^2 V}{\partial x^2} + \frac{\partial^2 V}{\partial y^2} \; . $$
Hvilke av disse funksjonene kan tilfredsstille Laplace likning?
h) \( V(x,y) = Ax + By \)
Ja
i) \( V(x,y) = A \sin x + B \sin y \)
Nei
j) \( V(x,y) = A \, e^{-y} \, \sin x \).
Ja