Oppgave
Oppgave: Maksimal fluks
Et uniformt elektrisk felt er rettet langs \( x \)-aksen: \( \vec{E} = E_0 \x \).
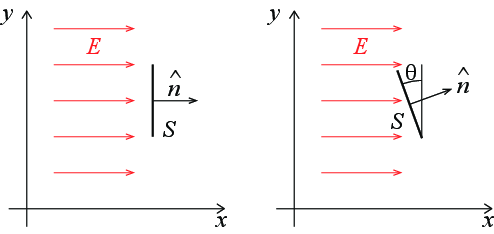
Figuren til venstre viser en orientert overflate \( \vec{S} \).
a) Hva er fluksen gjennom denne overflaten?
\( E_0 S \)
Fluksen er \( \Phi = \vec{E} \cdot \vec{S} = E_x \x \cdot S \x = E_0 S \)
Figuren til høyre viser en orientert overflate \( \vec{S} \) som har en vinkel \( \theta \) med \( y \)-aksen.
b) For hvilken vinkel \( \theta \) er fluksen størst?
\( \theta = 0 \)
c) For hvilken vinkel er fluksen minst?
\( \theta = \pi \).
d) Finn et uttrykk for fluksen som funksjon av \( \theta \).
\( \Phi = E_0 S\cos \theta \)
Vi finner \( \Phi \) fra \( \Phi = \vec{E} \cdot \vec{S} = E_0 \x \cdot \hat{n} \) hvor \( \hat{n} = (\cos \theta, \sin \theta) \) slik at \( \Phi = E_0 \cos \theta \). Vi ser at \( \Phi \) er maksimal når \( \theta = 0 \) og minimal når \( \theta = \pi \).