Oppgave
Oppgave: Flere plan
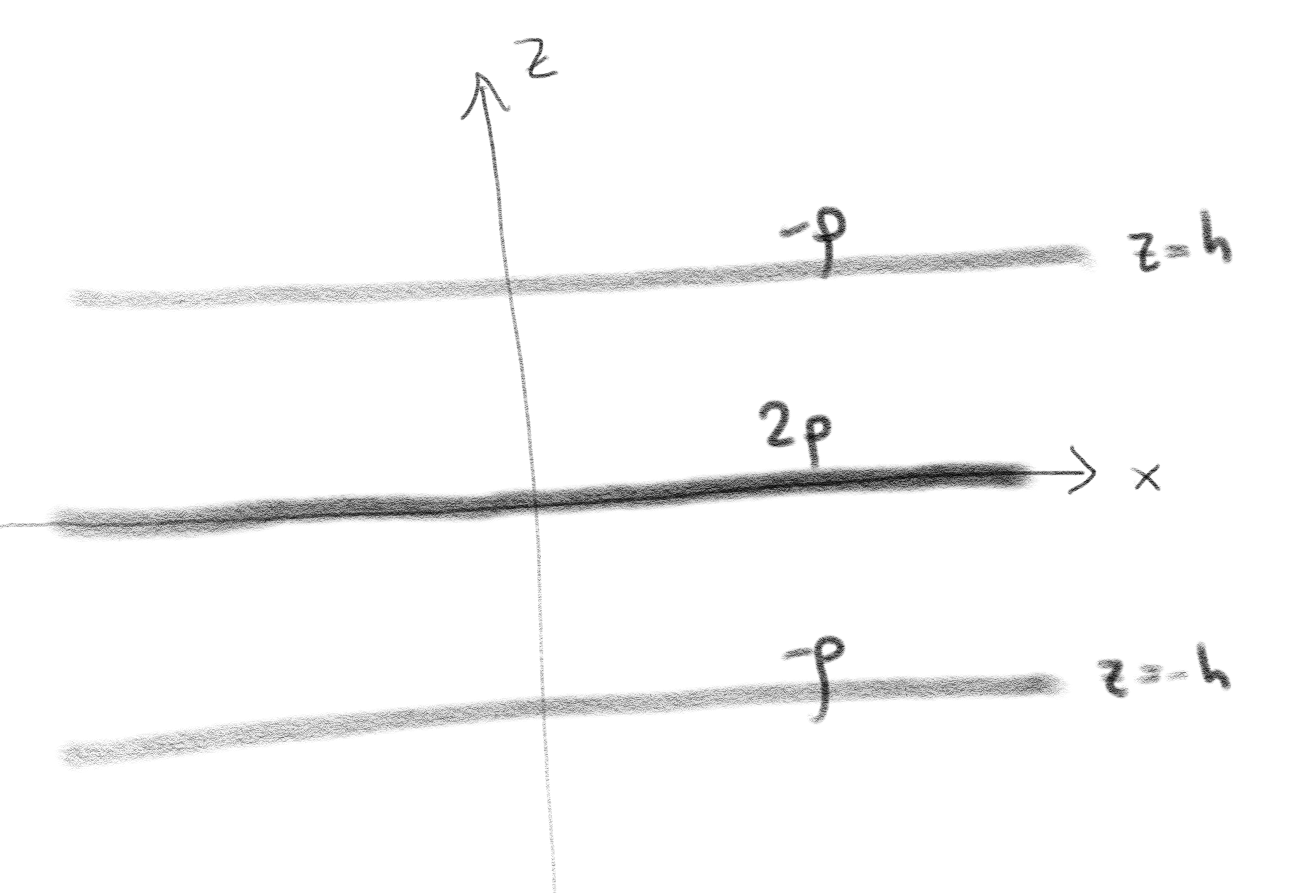
Vi plasserer tre plan over hverandre. Et plan gjennom \( z = 0 \) med ladningstetthet \( 2 \rho \), ett plan gjennom \( z=h \) med ladningstetthet \( -\rho \) og ett plan gjennom \( z=-h \) med ladningstetthet \( -\rho \).
a) Skisser systemet
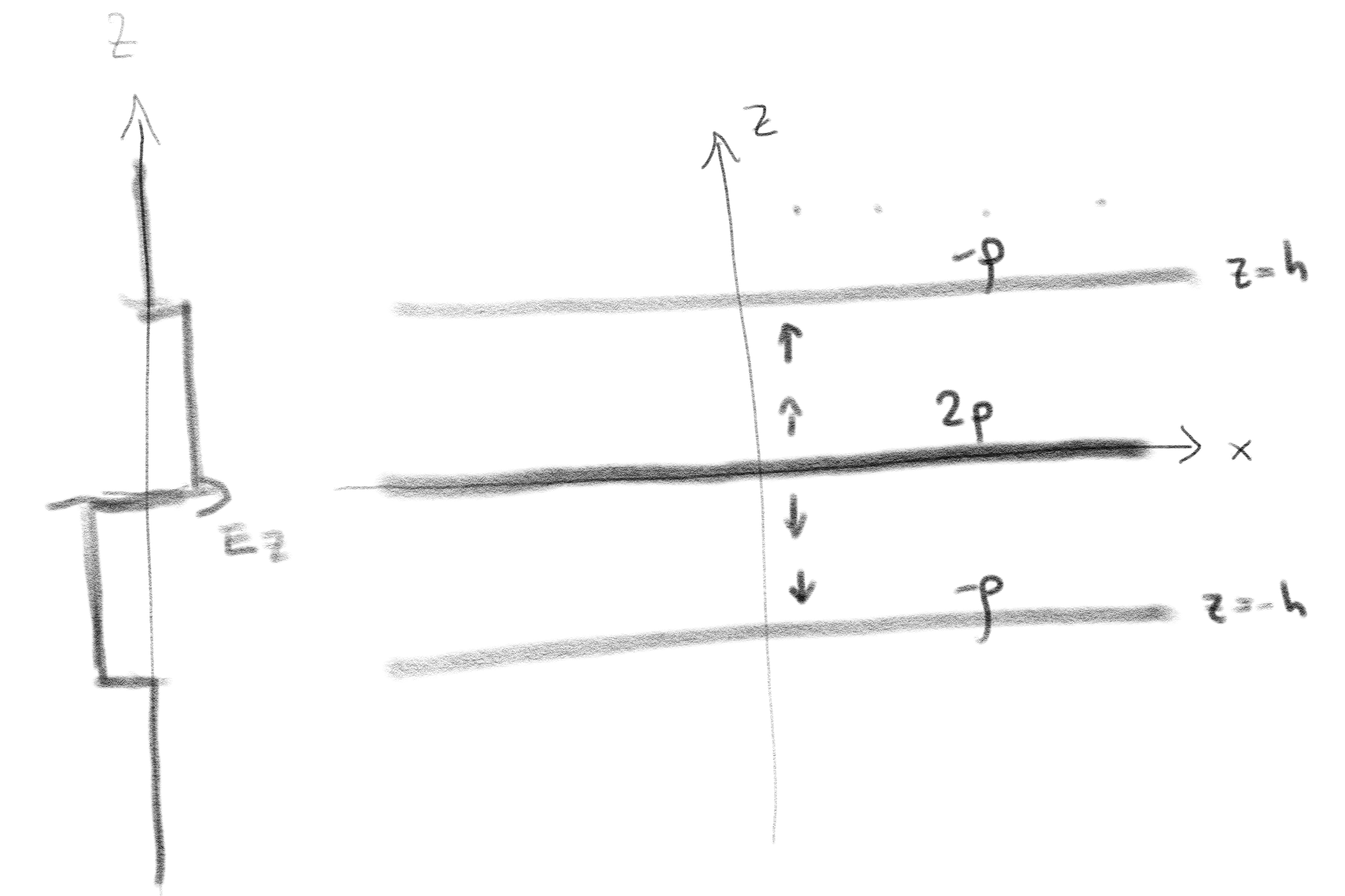
b) Skisser det elektriske feltet som funksjon av \( z \).
c) Regn ut det elektriske feltet som funksjon av \( z \).
Vi bruker Gauss' lov til å finne det elektriske feltet fra en plate med overflateladningstetthet \( \rho \). Fra symmetri ser vi at feltet kun vil ha en komponent i \( z \)-retningen og at den kun kan avhenge av \( z \), slik at \( \vec{E} = E_z(z) \z \). Dessuten vil \( E_z(z) = -E_z(-z) \).
Vi plasserer en Gaussflate symmetrisk omkring platen med en overflate \( A \) i avstanden \( z \) og tilsvarende \( -z \). Da gir Gauss' lov at $$ \int_S \vec{E} \cdot \d \vec{S} = E_z(z)A - E_z(-z)A = 2 E_z A = \frac{A \rho}{\epsilon_0} \quad \Rightarrow \quad E_z = \frac{\rho}{2\epsilon_0}$$
Utenfor platene er det elektriske feltet null, fordi netto ladning innenfor en Gaussflate vil være null. I området mellom platene vil feltene fra den øverste og den nederste platen kansellere hverandre. Feltet blir derfor det samme som feltet fra den midterste platen som er \( E_z = \frac{2\rho}{2 \epsilon_0} = \frac{\rho}{\epsilon_0} \).